Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước 1:
Từ HĐ 1 ta có hai bất phương trình:
\(x + 2y \ge 400\left( 1 \right)\) và \(x + 2y < 400\left( 2 \right)\)
Thay x=100 và y=100 vào bất phương trình (1) ta được:
\(100 + 2.100 \ge 400 \Leftrightarrow 300 \ge 400\) (Vô lí)
=> Cặp số (x;y)=(100;100) không thỏa mãn bất phương trình (1).
Thay x=100 và y=100 vào bất phương trình (2) ta được:
\(100 + 2.100 < 400 \Leftrightarrow 300 < 400\) (Đúng)
=> Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2).
Cặp số (x;y)=(100;100) thỏa mãn bất phương trình (2) có nghĩa là nếu bán được 100 vé loại 1 và 100 vé loại 2 thì rạp chiếu phim phải bù lỗ.
Bước 2:
Thay x=150 và y=150 vào bất phương trình (1) ta được:
\(150 + 2.150 \ge 400 \Leftrightarrow 450 \ge 400\) (Đúng)
=> Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1).
Thay x=150 và y=150 vào bất phương trình (2) ta được:
\(150 + 2.150 < 400 \Leftrightarrow 450 < 400\) (Vô lí)
=> Cặp số (x;y)=(150;150) không thỏa mãn bất phương trình (2).
Cặp số (x;y)=(150;150) thỏa mãn bất phương trình (1) có nghĩa là nếu bán được 150 vé loại 1 và 150 vé loại 2 thì rạp chiếu phim không phải bù lỗ.
Chú ý
Khi thay cặp số (x;y)=(100;100) vào các bất phương trình bài cho đồng nghĩa với rạp chiếu phim bán được 100 vé loại 1 và 100 vé loại 2.

gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)

Gọi x là số vé loại 1 bán được và y là số vé loại 2 bán được. \((x,y \in \mathbb N)\)
Số tiền bán vé thu được là: \(50000x + 100000y\) (đồng)
Rạp chiếu phim phải bù lỗ nếu: \(50000x + 100000y < 20 000 000\)
\(\Leftrightarrow x + 2y < 400\)
Vậy rạp chiếu phim phải bù lỗ nếu số vé mỗi loại thỏa mãn biểu thức \(x + 2y < 400\).

Tham khảo:
a)
Bước 1: Ta có:
| Loại A | Loại B |
Giá mua vào | 10 triệu đồng/1 máy | 20 triệu đồng/1 máy |
Lợi nhuận | 2,5 triệu đồng/1 máy | 4 triệu đồng/1 máy |
Bước 2: Lập hệ bất phương trình
Vì số lượng máy là số tự nhiên nên ta có \(x \ge 0;y \ge 0\)
Vốn nhập vào x máy loại A và y máy loại B là \(10x + 20y\)(triệu đồng)
4 tỉ đồng=4000 (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có bất phương trình
\(10x + 20y \le 4000\) \( \Leftrightarrow x + 2y \le 400\)
Vì tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy nên ta có \(x + y \le 250\).
Vậy ta có hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Bước 3: Xác định miền nghiệm
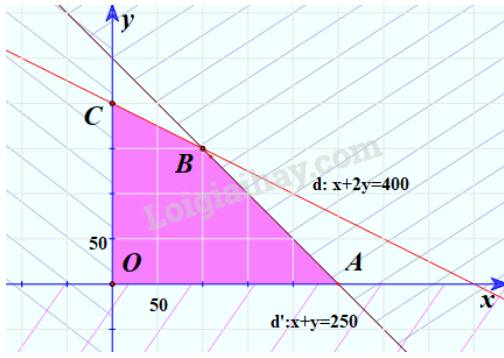
Miền nghiệm là tứ giác OABC với tọa độ các đỉnh này là O(0;0), A(250;0), B(100;150), C(0;200)
b) Lợi nhuận hàng tháng là F(x;y)=2,5x+4y(triệu đồng)
c) Ta cần tìm giá trị lớn nhất của F(x;y) khi (x;y) thỏa mãn hệ bất phương trình \(\left\{ \begin{array}{l}x \ge 0\\y \ge 0\\x + 2y \le 400\\x + y \le 250\end{array} \right.\)
Ta có F(0;0)=0, F(250;0)=2,5.250+4.0=625
F(100;150)=2,5.100+4.150=850
F(0;200)=2,5.0+4.200=800
Giá trị lớn nhất là F(100;150)=850.
Vậy cửa hàng cần đầu tư kinh doanh 100 máy A và 150 máy B.
a) Số máy tính loại A cửa hàng cần nhập trong một tháng là x (máy), số máy tính loại B cửa hàng cần nhập trong một tháng là y (máy) (x,y≥0).
Do tổng nhu cầu hàng tháng sẽ không vượt quá 250 máy: x + y ≤ 250
Tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì mỗi chiếc máy tính loại A có giá 10 triệu và mỗi máy tính loại B có giá 20 triệu nên tổng số vốn cửa hàng cần nhập hai loại A và B: 10x + 20y (triệu đồng)
Vì số vốn ban đầu không vượt quá 4 tỉ đồng nên ta có: 10x + 20y ≤ 4 000 hay x + 2y ≤ 400.
Ta có hệ bất phương trình: \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Ta xác định miền nghiệm của hệ bất phương trình trên:
+) Miền nghiệm D1 của bất phương trình x ≥ 0 là nửa mặt phẳng bờ Oy chứa điểm (1;0).
+) Miền nghiệm D2 của bất phương trình y ≥ 0 là nửa mặt phẳng bờ Ox chứa điểm (0;1).
+) Xác định miền nghiệm D3 của bất phương trình x + y ≤ 250.
- Vẽ đường thẳng d: x + y = 250.
- Vì 0 + 0 = 0 < 250 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + y ≤ 250
Do đó miền nghiệm D3 của bất phương trình x + y ≤ 250 là nửa mặt phẳng bờ d chứa gốc tọa độ.
+) Xác định miền nghiệm D4 của bất phương trình x + 2y ≤ 400.
- Vẽ đường thẳng d’: x + 2y = 400.
- Vì 0 + 2.0 = 0 < 400 nên tọa độ điểm O(0;0) thỏa mãn bất phương trình x + 2y < 400
Do đó miền nghiệm D4 của bất phương trình x + 2y < 400 là nửa mặt phẳng bờ d’ chứa gốc tọa độ.
Miền nghiệm của hệ bất phương trình trên là tứ giác OABC với O(0;0), A(0; 200), C(100;150), B(250;0)
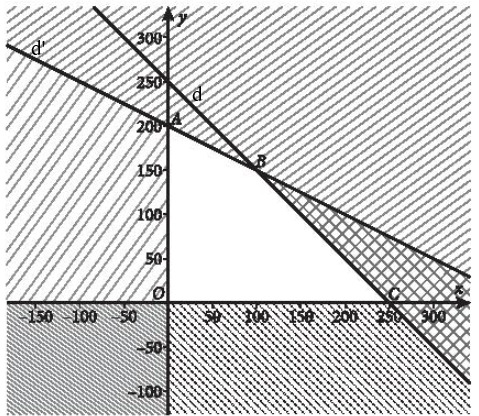
b) Lợi nhuận mà cửa hàng thu được trong tháng đó khi bán x máy tính loại A và y máy tính loại B là: F(x;y) = 2,5x + 4y (triệu đồng).
Vậy F(x;y) = 2,5x + 4y.
c) Bài toán chuyển về tìm giá trị lớn nhất của F(x;y) với (x;y) thuộc miền nghiệm của hệ bất phương trình \(\left\{{}\begin{matrix}x\ge0\\y\ge0\\x+y\le250\\x+2y\le400\end{matrix}\right.\)
Người ta đã chứng minh được, giá trị F(x; y) lớn nhất tại (x; y) là tọa độ của một trong bốn đỉnh O; A; B; C.
Tại O(0; 0), ta có: F(0; 0) = 2,5 . 0 + 4 . 0 = 0;
Tại A(0; 200), ta có: F(0; 200) = 2,5 . 0 + 4 . 200 = 800;
Tại B(100; 150), ta có: F(100; 150) = 2,5 . 100 + 4 . 150 = 850;
Tại B(250; 0), ta có: F(250; 0) = 2,5 . 250 + 4 . 0 = 625.
Do đó F(x;y) lớn nhất bằng 850 tại x = 100 và y = 150.
Vậy cửa hàng cần nhập 100 máy loại A, 150 máy loại B để cửa hàng thu được lợi nhuận lớn nhất là 850 triệu đồng.

Số tiền mua x chiếc điều hòa hai chiều là 20x (triệu đồng)
Số tiền mua y chiếc điều hòa một chiều là 10y (triệu đồng).
Số tiền khi mua x chiếc điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
a) Nhu cầu thị trường không quá 100 máy cả 2 loại có nghĩa là tổng số điều hòa nhập vào cũng không quá 100 máy: \(x + y \le 100\)
b)
1,2 tỉ đồng =1200 (triệu đồng)
Số vốn mua x điều hòa hai chiều và y chiếc điều hòa một chiều là 20x+10y (triệu đồng).
Do chủ cửa hàng có thể đầu tư không vượt quá 1,2 tỉ đồng nên ta có: \(20x + 10y \le 1200\)
\( \Leftrightarrow 2x + y \le 120\)
c)
Số tiền lãi khi bán x chiếc điều hòa hai chiều là 3,5x (triệu đồng)
Số tiền lãi khi bán y chiếc điều hòa một chiều là 2y (triệu đồng)
Tổng số tiền lãi là 3,5x+2y (triệu đồng)

TRẢ LỜI:
Gọi x, y, z lần lượt là số đồng tiền xu loại 2000 đồng, 1000 dồng, 500 đồng.
Điều kiện là x, y, z nguyên dương
Ta có hệ phương trình
x + y + z = 1450 (1)
4x + 2y + z = 3000 (2)
2x + y - 2z = 0 (3)
Trừ từng vế tương ứng của phương trình (2) với phương trình (1) ta được
3x + y = 1550
Cộng từng vế tương ứng của các phương trình (1), (2) và (3) ta có :
7x + 4y = 4450.
Giải hệ gồm hai phương trình (4) và (5) ta được.
x = 350, y = 500.
Thay các giá trị của x, y vào phương trình (1) ta được z = 600.
Vậy cửa hàng đổi được 350 đồng tiền xu loại 2000 đồng, 500 đồng tiền loại 1000 đồng và 600 đồng tiền xu loại 500 đồng.


Bước 1:
Số tiền bán x vé loại 1 là: \(x.50\) (nghìn đồng)
Số tiền bán y vé loại 2 là: \(y.100\) (nghìn đồng)
Bước 2:
Số tiền thu được là
\(50x + 100y\) (nghìn đồng)
a)
Ta có 20 triệu = 20 000 (nghìn đồng)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Nên để số tiền thu được tối thiểu 20 triệu thì ta cần:
\(\begin{array}{l}50x + 100y \ge {20 000}\\ \Leftrightarrow x + 2y \ge 400\end{array}\)
Vậy các số nguyên không âm x và y phải thỏa mãn điều kiện \(x + 2y \ge 400\)
b)
Số tiền thu được khi bán x vé loại 1 và y vé loại 2 là \(50x + 100y\) (nghìn đồng)
Số tiền thu được nhỏ hơn 20 triệu thì:
\(\begin{array}{l}50x + 100y < {20 000}\\ \Leftrightarrow x + 2y < 400\end{array}\)
Chú ý:
- Số tiền tối thiểu thì ta phải lập bất phương trình với dấu “\( \ge \)”.
- Cần đổi 20 triệu đồng thành 20 000 nghìn đồng tránh lập sai bất phương trình.