Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

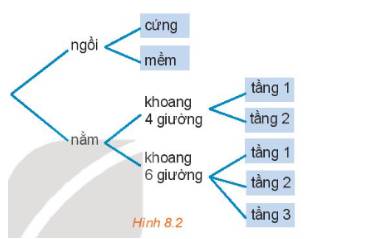
a) Số vé ghế ngồi là 2 (loại vé)
Số vé giường nằm là 2 + 3 = 5 (loại vé)
b) Số loại vé để bạn An lựa chọn là:
2 + 5 = 7 (loại vé)

Lời giải:
Giả sử ban đầu có $a$ dãy ghế thì mỗi dãy có $b$ người. Trong đó $a,b$ là số tự nhiên $\neq 0$. Ta có: $ab=150(1)$
Khi thêm 71 người thì có tổng $150+71=221$ người.
Số dãy ghế: $a+2$
Số người mỗi dãy: $b+3$
Ta có: $(a+2)(b+3)=221(2)$
Từ $(1); (2)\Rightarrow 3a+2b=65$
$\Rightarrow b=\frac{65-3a}{2}$. Thay vào $(1)$ thì:
$a.\frac{65-3a}{2}=150$
$\Leftrightarrow a(65-3a)=300$
$\Leftrightarrow 3a^2-65a+300=0$
$\Leftrightarrow a=15$ (chọn) hoặc $a=\frac{20}{3}$ (loại)
Vậy có $15$ dãy ghế.

+) Xếp 4 bạn vào 4 ghế là sự hoán vị của 4 phần tử. Do đó, không gian mẫu là: \(n\left( \Omega \right) = 4!\) ( phần tử)
a) +) Gọi A là biến cố “Bạn Thảo ngồi ghế đầu tiên”
Ghế đầu tiên là ghế của Thảo nên có 1 cách chọn, 3 ghế còn lại xếp tùy ý 3 bạn nên ta có sự hoán vị của 3 phần tử. Theo quy tắc nhân, ta có: \(n\left( A \right) = 1.3!\) ( phần tử)
+) Vậy xác suất của biến cố A là: \(P\left( A \right) = \frac{{n\left( A \right)}}{{n\left( \Omega \right)}} = \frac{1}{4}\)
b) +) Gọi B là biến cố “Bạn Thảo ngồi ghế đầu tiên và bạn Huy ngồi ghế cuối cùng”.
Ghế đầu tiên của bạn Thảo và ghế cuối cùng của bạn Huy nên có 1 cách chọn cho cả 2 ghế, 2 ghế còn lại xếp tùy ý 2 bạn nên ta có sự hoán vị của 2 phần tử. Theo quy tắc nhân, ta có: \(n\left( B \right) = 1.1.2!\) ( phần tử)
+) Vậy xác suất của biến cố B là: \(P\left( B \right) = \frac{{n\left( B \right)}}{{n\left( \Omega \right)}} = \frac{1}{{12}}\)

Mỗi cách sắp xếp 6 bạn vào 6 chiếc ghế trống là hoán vị của 6 chiếc ghế. Do đó, số cách sắp xếp chỗ ngồi cho các thành viên trong nhóm là
\({P_6} = 6! = 720\) (cách)

Gọi số xe chở 3 tấn, chở 5 tấn và xe chở 7,5 tấn lần lượt là:\(x,y,z\left(x,y,z\in N;x,y,z>0\right)\).
Do tổng số xe là 57 nên: \(x+y+z=57\).
Số tấn xi măng phải chở là 290 tấn nên: \(3x+5y+7,5z=290\).
Tất cả số xe chở 7,5 tấn chở 3 chuyến được: \(3.7,5.z\).
Tất cả số xe 5 tấn chở 3 chuyến và số xe 3 tấn chở 2 chuyến được: \(3.5.y+2.3x\).
Ta có phương trình: \(3.7,5z=3.5y+2.3x\Leftrightarrow22,5z=15y+6x\)
Ta có hệ phương trình:
\(\left\{{}\begin{matrix}x+y+z=57\\3x+5y+7,5z=290\\22,5z=15y+6x\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=20\\y=19\\z=18\end{matrix}\right.\)
Vậy số xe 3 tấn là 20 xe, số xe 5 tấn là 19 chiếc, số xe 7,5 tấn là 18 xe.

Gọi x là số xe tải chở 3 tấn, y là số xe chở 5 tấn và z là số xe tải chở 7,5 tấn. Điều kiện x, y, z nguyên dương.
Theo giả thiết của bài toán ta có:
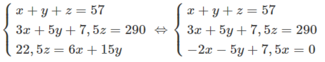
Cộng từng vế phương trình thứ hai với phương trình thứ ba ta được hệ phương trình
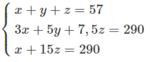
Nhân hai vế của phương trình thứ nhất với -5 rồi cộng từng vế với phương trình thứ hai ta được
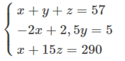
Từ phương trình cuối suy ra x = 290 – 15z
Thay giá trị tìm được của x vào phương trình thứ hai ta được 32,5z = 585 hay z = 18.
Từ đó suy ra x = 20, y = 19. Các giá trị của x, y, z vừa tìm được thỏa mãn điều kiện của bài toán.
Vậy có 20 xe chở 3 tấn, 19 xe chở 5 tấn và 18 xe chở 7,5 tấn.



gọi \(x\times100000\text{ là số tiền vé đã tăng}\)
khi đó \(\hept{\begin{cases}\text{Giá vé khi đó là : }100000\times\left(x+4\right)\\\text{số người trên xe khi đó là : }60-10\times x=10\times\left(6-x\right)\end{cases}}\)
khi đó tổng số tiền bán vé thu được là :
\(100000\times\left(x+4\right)\times10\times\left(6-x\right)=1.000.000\times\left(4+x\right)\times\left(6-x\right)\)
\(\le1.000.000\times\left(\frac{4+x+6-x}{2}\right)^2=25.000.000\)
dấu "=" xảy ra khi \(x+4=6-x\Leftrightarrow x=1\)