Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Txđ: D =\(\left[1998;+\infty\right]\)
b) \(f\left(2002\right)=620000\) con.
\(g\left(1999\right)=380000\) con.
\(h\left(2000\right)=100000\) con.
c) \(h\left(1999\right)=30000\) con; \(h\left(2002\right)=210000\).
\(h\left(2002\right)-h\left(1999\right)=210000-30000=180000\).
Ý nghĩa: Hiệu \(h\left(2002\right)-h\left(1999\right)\) thể hiện sự tăng trưởng sản lượng ngan qua giai đoạn 1999 - 2002.

a) Hệ số a là: a=1
\(f(0) = {0^2} - 4.0 + 3 = 3\)
\(f(1) = {1^2} - 4.1 + 3 = 0\)
\(f(2) = {2^2} - 4.2 + 3 = - 1\)
\(f(3) = {3^2} - 4.3 + 3 = 0\)
\(f(4) = {4^2} - 4.4 + 3 = 3\)
=> f(0); f(4) cùng dấu với hệ số a; f(2) khác dấu với hệ số a
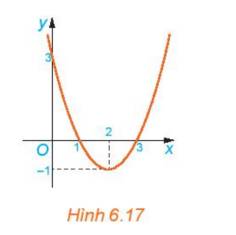
b) Nhìn vào đồ thị ta thấy
- Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành
c) - Trên khoảng \(\left( { - \infty ;1} \right)\) đồ thị nằm phía trên trục hoành => f(x)>0, cùng dầu với hệ số a
- Trên khoảng \(\left( {1;3} \right)\), đồ thị nằm phía dưới trục hoành => f(x) <0, khác dấu với hệ số a
- Trên khoảng \(\left( {3; + \infty } \right)\), đồ thị nằm phía trên trục hoành => f(x)>0, cùng dấu với hệ số a

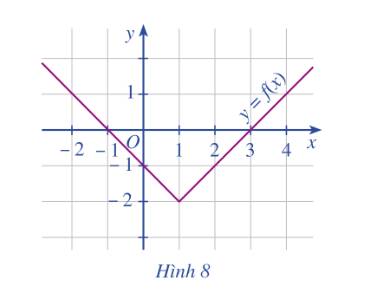
a) Quan sát đồ thị:
điểm \(\left( {1; - 2} \right)\) (tức là có x =1; y=-2) thuộc đồ thị.
điểm \(\left( {2; - 1} \right)\) (tức là có x=2; y=-1) thuộc đồ thị hàm số.
điểm (0;0) không thuộc đồ thị hàm số.
b) Từ điểm trên Ox: \(x = 0\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 0 \right) = - 1\)
Từ điểm trên Ox: \(x = 3\) ta kẻ đường thẳng song song với Oy ta được: \(f\left( 3 \right) = 0\)
c) Giao điểm của đồ thị và trục Ox là điểm \(\left( {3;0} \right)\).

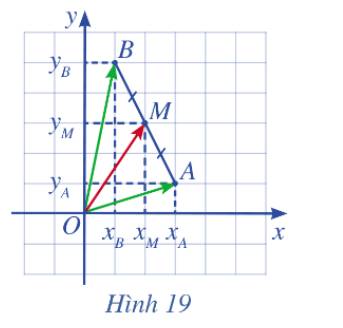
a) Ta có vectơ \(\overrightarrow {OM} \) biểu diễn theo hai vectơ \(\overrightarrow {OA} \) và \(\overrightarrow {OB} \) là: \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right)\)
b) Do tọa độ hai điểm A và B là: \(A\left( {{x_A},{y_A}} \right),B\left( {{x_B},{y_B}} \right)\) nên ta có:\(\overrightarrow {OA} = \left( {{x_A},{y_A}} \right),\overrightarrow {OB} = \left( {{x_B},{y_B}} \right)\)
Vậy \(\overrightarrow {OM} = \frac{1}{2}\left( {\overrightarrow {OA} + \overrightarrow {OB} } \right) = \frac{1}{2}\left( {{x_A} + {x_B};{y_A} + {y_B}} \right) = \left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)
Tọa độ điểm M chính là tọa độ của vectơ nên tọa độ M là \(M\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2}} \right)\)

a) F(x) = \(-x^2\left(x-1\right)\left(x+2\right)\left(x+2\right)=\left(1-x\right)x^2\left(x+2\right)^2\\ \)
\(\left\{{}\begin{matrix}x^2\ge0\\\left(x+2\right)^2\ge0\end{matrix}\right.\) => dấu biểu thức chỉ phụ thuộc vào thừa số (1-x)
F(x) =0 khi x={-2,0,1}
F(x) > 0 khi x<1 và khác -2 và 0
f(x) <0 khi x> 1
Tử f(x) =x^2(x^2-3x+2) =x^2(x-1)(x-2)
tương tự a) dấu của tử phụ thuộc (x-1)(x-2)
Mẫu f(x) =x^2 -x-30 =(x-5)(x+6)
Phần hỗ trợ Lập bảng đây khó thao tác
=> viết bằng hệ {điểm tới hạn xet x={-6,0,1,2,5}
Khi => \(\left[{}\begin{matrix}x=0\\x=1\\x=2\end{matrix}\right.\)=>f(x) =0
Khi \(\left[{}\begin{matrix}x=5\\x=-6\end{matrix}\right.\) => f(x) không xác định
Khi \(x< -6\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\)\(\Rightarrow f\left(x\right)>0\)
khi -6<x<1 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi 1<x<2 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)< 0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) >0
khi 2<x<5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)< 0\end{matrix}\right.\) => f(x) <0
khi x>5 \(\Rightarrow\left\{{}\begin{matrix}Tf\left(x\right)>0\\Mf\left(x\right)>0\end{matrix}\right.\) => f(x) >0

a) Biểu thức \(f\left( x \right) = 2{x^2} + x - 1\) là một tam thức bậc hai
\(f\left( 1 \right) = {2.1^2} + 1 - 1 = 2 > 0\) nên \(f\left( x \right)\) dương tại \(x = 1\)
b) Biểu thức \(g\left( x \right) = - {x^4} + 2{x^2} + 1\) không phải là một tam thức bậc hai
c) Biểu thức \(h\left( x \right) = - {x^2} + \sqrt 2 .x - 3\) là một tam thức bậc hai
\(h\left( 1 \right) = - {1^2} + \sqrt 2 .1 - 3 = \sqrt 2 - 4 < 0\) nên \(h\left( x \right)\) âm tại \(x = 1\)
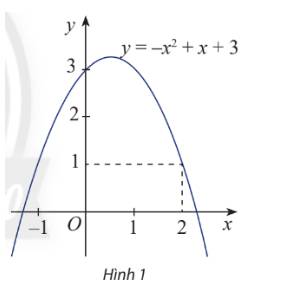

a) Số mũ cao nhất của hàm số là 2, suy ra biểu thức\(f\left( x \right)\)đã cho là đa thức bậc hai
b) Thay \(x = 2\) vào \(f\left( x \right)\) ta có:
\(f\left( 2 \right) = - {2^2} + 2 + 3 = 1 > 0\)
Suy ra \(f\left( 2 \right)\) dương.