
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: XetΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
=>BA=BH; DA=DH
mà DH<DC
nên DA<DC
b: Xét ΔBHK vuông tại H và ΔBAC vuông tại A có
BH=BA
góc B chung
=>ΔBHK=ΔBAC
=>BK=BC
c: ΔBKC cân tại B
mà BD là phân giác
nên BD là trung trực của KC

Bài 1:
a,b: ΔABC cân tại A
mà AM là trung tuyến
nên AM vừa là đường cao, vừa là phân giác
=>góc BAM=góc CAM và AM vuông góc với BC
c: Xét ΔEBC có
EM vừa là đường cao, vừa là trung tuyến
nên ΔEBC cân tại E
d: Xét ΔKCB có
CE là trung tuyến
CE=KB/2
Do đó: ΔKCB vuông tại C
=>KC//AE

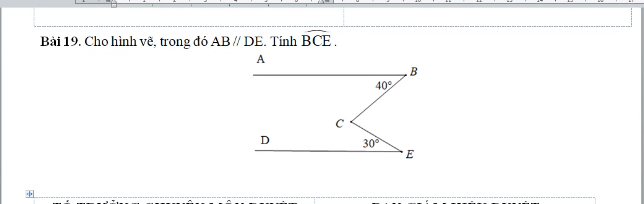
Kẻ CF//AB thì CF//DE
Do đó \(\widehat{BCF}=\widehat{ABC}=40^0;\widehat{FCE}=\widehat{CED}=30^0\) (so le trong)
Vậy \(\widehat{BCE}=\widehat{BCF}+\widehat{FCE}=30^0+40^0=70^0\)

1. Do góc BOC kề bù với góc AOB
=> Tia OA và tia OC đối nhau
Do góc AOD và góc AOB kề bù
=> tia OD và tia OB đối nhau
=> góc BOC và góc AOD là 2 góc đối đỉnh
Gọi OM, ON là 2 tia phân giác góc AOD và góc BOC
=> góc AOM = 1/2 góc AOD = 1/2 (180* - 135*) = 45*/2
mà góc AON = góc AOB + góc BON
=> góc AON = 135* + 45*/2
=> góc AOM + góc AON = 135* + 45*/2 + 45*/2 = 180*
=> góc MON = 180*
=> OM , ON là 2 tia đối nhau


Bài 5:
a: a//c
a\(\perp\)b
Do đó: b\(\perp\)c
b: ta có: a//c
=>\(\widehat{A_4}=\widehat{B_2}\)(hai góc so le trong)
mà \(\widehat{A_4}=45^0\)
nên \(\widehat{B_2}=45^0\)
Ta có: \(\widehat{B_2}+\widehat{B_1}=180^0\)(hai góc kề bù)
=>\(\widehat{B_1}+45^0=180^0\)
=>\(\widehat{B_1}=180^0-45^0=135^0\)
Câu 6:
a: Xét ΔABM và ΔACM có
AB=AC
BM=CM
AM chung
Do đó: ΔAMB=ΔAMC
=>\(\widehat{AMB}=\widehat{AMC}\)
mà \(\widehat{AMB}+\widehat{AMC}=180^0\)(hai góc kề bù)
nên \(\widehat{AMB}=\widehat{AMC}=\dfrac{180^0}{2}=90^0\)
=>AM\(\perp\)BC
b: Xét ΔABC có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
nên DE//BC
c: Xét tứ giác MCFE có
G là trung điểm chung của MF và CE
=>MCFE là hình bình hành
=>EF//MC
=>EF//BC
Ta có: EF//BC
DE//BC
EF,DE có điểm chung là E
Do đó: D,E,F thẳng hàng

a: Xét ΔBAE vuông tại A và ΔBIE vuông tại I có
BE chung
\(\widehat{ABE}=\widehat{IBE}\)
Do đó: ΔBAE=ΔBIE
Suy ra: BA=BI
hay ΔBIA cân tại B
b: Ta có: ΔBAE=ΔBIE
nên EA=EI
hay E nằm trên đường trung trực của AI(1)
Ta có: BA=BI
nên B nằm trên đường trung trực của AI(2)
Từ (1) và (2) suy ra BE là đường trung trực của AI
hay BE\(\perp\)AI
c: Xét ΔAEK vuông tại A và ΔIEC vuông tại I có
EA=EI
\(\widehat{AEK}=\widehat{IEC}\)
Do đó:ΔAEK=ΔIEC
Suy ra: AK=IC
Ta có: BA+AK=BK
BI+IC=BC
mà BA=BI
và AK=IC
nên BK=BC
hay ΔBKC cân tại B
d: Xét ΔBKC có BA/BK=BI/BC
nên AI//KC



 giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ
giúp mk với, mk cần gấp, mn nêu cả lời giải chi tiêt 1 chút giúp mk nhé, cam on mn rất nhìu ạ
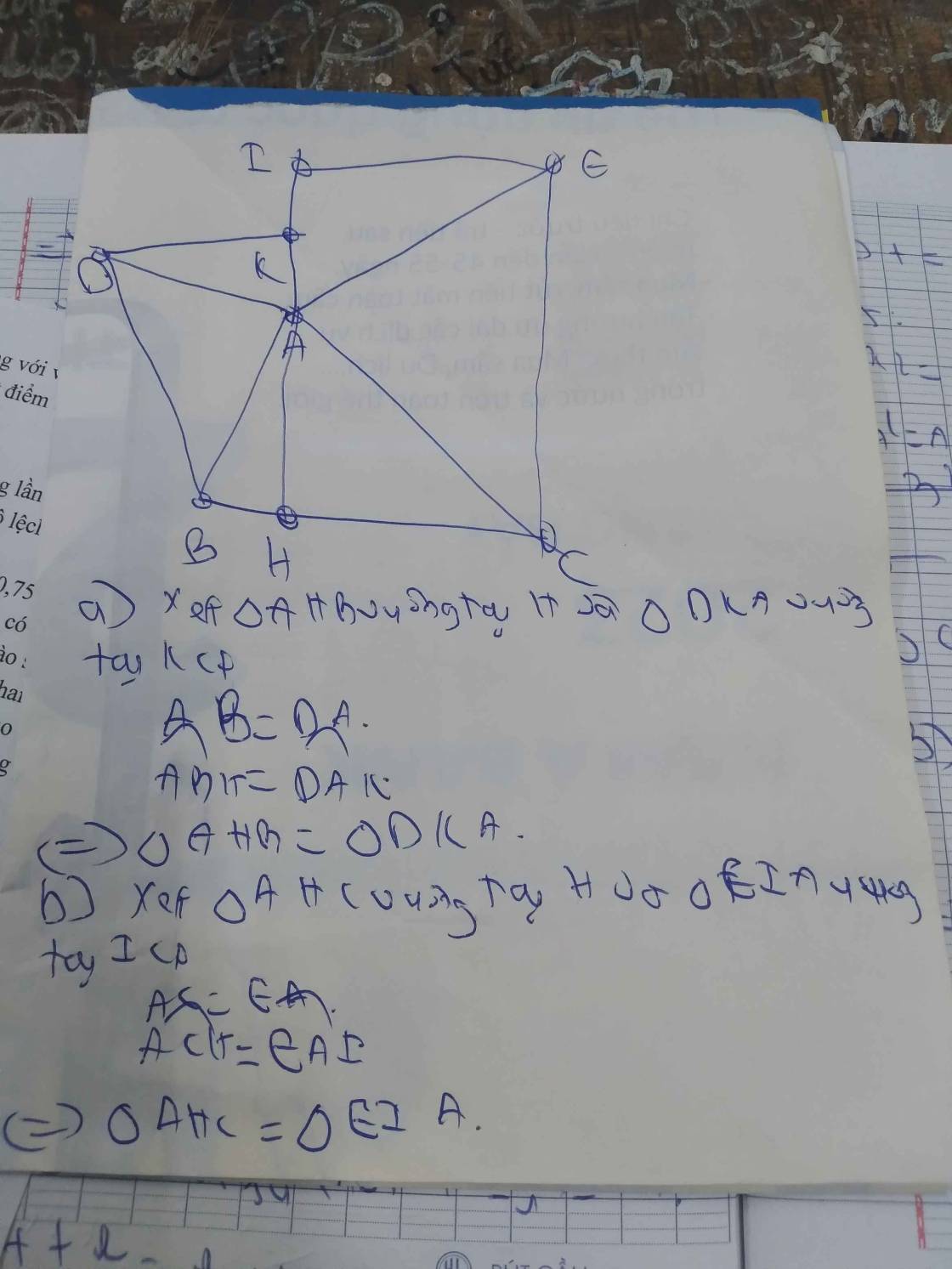


 vẽ hình bài6 và làm 2 bài này giúp ạ
vẽ hình bài6 và làm 2 bài này giúp ạ 
a: Xét ΔMHC và ΔMKB có
MH=MK
góc HMC=góc KMB
MC=MB
=>ΔMHC=ΔMKB
b: ΔMHC=ΔMKB
=>BK=HC<MC
c: Xét ΔCAB có
M là trung điểm của CB
MH//AB
=>H là trung điểm của AC
Xét ΔCAB có
AM,BH là trung tuyến
AM cắt BH tại G
=>G là trọng tâm
=>C,G,I thẳng hàng