Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔAHB vuông tại H và ΔDHB vuông tại H có
BA=BD(Gt)
BH chung
Do đó: ΔAHB=ΔDHB(cạnh huyền-cạnh góc vuông)
Suy ra: AH=DH(hai cạnh tương ứng)
Xét ΔAKC vuông tại K và ΔEKC vuông tại K có
CA=CE(gt)
CK chung
Do đó: ΔAKC=ΔEKC(Cạnh huyền-cạnh góc vuông)
Suy ra: KA=KE(Hai cạnh tương ứng)
Xét ΔADE có
\(\dfrac{AH}{HD}=\dfrac{AK}{KE}\left(=1\right)\)
nên HK//DE(Định lí Ta lét đảo)

a) ta có AM=MD (gt)
BM=MC (AM là trung tuyến của tam giác)
Mà AD cắt BC tai M
=> ABCD là hình bình hành
Mà \(\widehat{BAC}=90^{\sigma}\) (gt)
=> ABCD là hình chữ nhật
b) ta có \(BI\perp AD\) (gt)
lại có \(CK\perp AD\) (gt)
=> BI // CK
bn coi lại câu c có sai đề k, nếu đúng thì mk chỉ lm đc 2 câu trên thôi!
Chọn mk nha

Gọi độ dài quãng đường AB là x
Theo đề, ta có: \(\dfrac{x}{35}=\dfrac{\dfrac{x}{2}}{35}+\dfrac{1}{4}+\dfrac{\dfrac{x}{2}}{40}\)
=>1/35x-1/70x-1/80x=1/4
=>x=2240

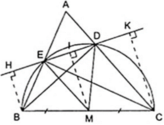
Vì BD, CE là đường cao của tam giác ABC nên
do đó Δ BDC vuông tại D, Δ CEB vuông tại E.
Gọi M là trung điểm của BC
⇒ DM, EM là đường trung tuyến ứng với cạnh huyền của Δ BDC và Δ CEB.
Áp dụng tính chất của đường trung tuyến ứng với cạnh huyền của hai tam giác trên ta được:
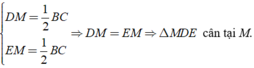
Từ giả thiết ta có tứ giác BHKC là hình thang vuông nên vẽ MI ⊥ DE thì BH//MI//CK ( 1 ) (vì cùng vuông góc với đường thẳng DE)
Mà ta có BM = MC ( 2 ) (do ta vẽ hình trên)
Từ ( 1 ),( 2 ) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK ( 3 ).
Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được:
EI = ID ( 4 )
Trừ theo vế đẳng thức ( 3 ) cho ( 4 ), ta được: HE = DK.

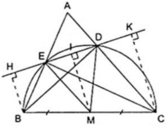
Vì BD, CE là đường cao của tam giác ABC nên do đó Δ BDC vuông tại D, Δ CEB vuông tại E.
do đó Δ BDC vuông tại D, Δ CEB vuông tại E.
Gọi M là trung điểm của BC
⇒ DM, EM là đường trung tuyến ứng với cạnh huyền của Δ BDC và Δ CEB.
Áp dụng tính chất của đường trung tuyến ứng với cạnh huyền của hai tam giác trên ta được: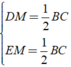
⇒ DM = EM ⇒ Δ MDE cân tại M.
Từ giả thiết ta có tứ giác BHKC là hình thang vuông nên vẽ MI ⊥ DE thì BH//MI//CK ( 1 ) (vì cùng vuông góc với đường thẳng DE)
Mà ta có BM = MC ( 2 ) (do ta vẽ hình trên)
Từ ( 1 ),( 2 ) suy ra BH, MI, CK là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng HK hai đoạn thẳng liên tiếp bằng nhau là HI = IK ( 3 ).
Áp dụng tính chất của đường cao ứng với cạnh đáy của tam giác cân MDE ta được:
EI = ID ( 4 ).
Trừ theo vế đẳng thức ( 3 ) cho ( 4 ), ta được: HE = DK.
Em ghi là đường cao H là sai, phải ghi là BH mới đúng vì vậy Olm bảo em làm sai em hiểu chưa nhỉ?