Question

[Pham Trong Bach]

Từ các chữ số thuộc tập X = {0;1;2;3;4;5;6;7} có thể lập được bao nhiêu số tự nhiên gồm 6 chữ số khác nhau sao cho mỗi số tự nhiên đó đều chia hết cho 18.

A. 720.

B. 860.

C. 984.

D. 1228.

Answer 1

[Cao Minh Tâm]

Chọn C

Giả sử số lập được có dạng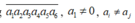 

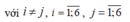
Ta có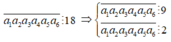 

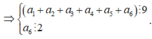
Vì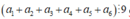  nên ta có các trường hợp sau

Trường hợp 1:  a 1 ,   a 2 ,   a 3 ,   a 4 ,   a 5 ,   a 6  được chọn từ 

+ Có 3 cách chọn chọn a 6

+ Có 5! cách chọn chọn bộ 5 số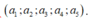 

Suy ra có 3.5! = 360 số.

Trường hợp 2:  a 1 ,   a 2 ,   a 3 ,   a 4 ,   a 5 ,   a 6   được chọn từ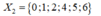 

+  a 6 = 0, có 5! cách chọn bộ 5 số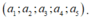 

+  a 6 ≠ 0 khi đó  a 6 có 3 cách chọn,  a 1 có 4 cách chọn và có 4! cách chọn bộ 4 số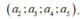 

Suy ra có 5! + 3.4.4!= 408 số

Trường hợp 3:  a 1 ,   a 2 ,   a 3 ,   a 4 ,   a 5 ,   a 6  được chọn từ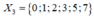 

+  a 6  = 0, có 5! cách chọn bộ 5 số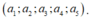 

+  a 6 ≠ 0 khi đó  a 6  có 1 cách chọn,   a 1  có 4 cách chọn và có 4! cách chọn bộ 4 số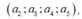 

Suy ra có 5! + 1.4.4! = 216 số

Vậy có: 360 + 408 + 216 = 984 số.