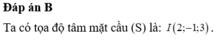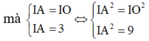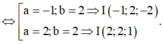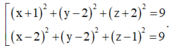Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
Gọi I là tâm mặt cầu (S). Khi đó I (t; 1+t; 2+t) và ta có:
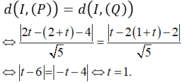
Vậy mặt cầu (S) có tâm I (1;2;3) và bán kính 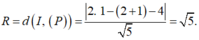
Do đó mặt cầu (S) có phương trình: ![]()

Đáp án A
Ta có (S): (x+1)²+(y-2)²+(z+3)²=16.
Do đó mặt cầu (S) có tâm I(-1;2;-3) và bán kính R=4.

Chọn D
Giả sử (S): x2 + y2 + z2 - 2ax - 2by - 2cz + d = 0 (a2 + b2 + c2 - d > 0)
![]() và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
và tâm I (a;b;c) ∈ (P) => a + b - c - 3 = 0 (1)
(S) qua A và O nên 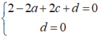
Cộng vế theo vế (1) và (2) ta suy ra b = 2. Từ đó, suy ra I (a; 2; a-1)
Chu vi tam giác OAI bằng 6 + √2 nên OI + OA + AI = 6 + √2
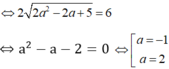
+ Với a = -1 => A (-1; 2; -2) => R = 3. Do đó:
![]()
+ Với a = 2 => I (2;2;1) => R = 3. Do đó:
![]()

Chọn D
Gọi vectơ pháp tuyến của mặt phẳng (P) là ![]() , a²+b²+c²>0.
, a²+b²+c²>0.
Phương trình mặt phẳng (P): a(x-4)+b (y-3)+c (z-4)=0.
Do (P) // Δ nên -3a+2b+2c=0 => 3a = 2 (b + c)
Mặt phẳng (P) tiếp xúc với (S) nên
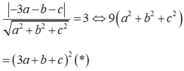
Thay 3a=2 (c+b ) vào (*) ta được:
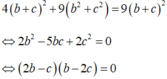
TH1: 2b-c=0, chọn b=1; c=2 => a = 2 => (P): 2x+y+2z-19=0 (thỏa).
TH2: b-2c=0, chọn c=1; b=2 => a = 2 => (P): 2x+2y+z-18=0 (loại do Δ ⊂ (P))

6.
Mặt phẳng Oxz có pt: \(y=0\)
Khoảng cách từ I đến Oxz: \(d\left(I;Oxz\right)=\left|y_I\right|=2\)
\(\Rightarrow R=2\)
Phương trình mặt cầu:
\(\left(x-1\right)^2+\left(y-2\right)^2+\left(z-3\right)^2=4\)
7.
Mặt phẳng (Q) nhận \(\left(1;-2;3\right)\) là 1 vtpt nên cũng nhận các vecto có dạng \(\left(k;-2k;3k\right)\) là vtpt
Bạn có ghi nhầm đề bài ko nhỉ? Thế này thì cả C và D đều ko phải vecto pháp tuyến của (Q)
4.
Đường thẳng d nhận \(\left(1;-2;2\right)\) là 1 vtcp
Gọi (P) là mặt phẳng qua M và vuông góc d \(\Rightarrow\) (P) nhận \(\left(1;-2;2\right)\) là 1 vtpt
Phương trình (P): \(1\left(x-2\right)-2\left(y-3\right)+2\left(z+1\right)=0\)
\(\Leftrightarrow x-2y+2z+6=0\)
Pt d dạng tham số: \(\left\{{}\begin{matrix}x=4+t\\y=1-2t\\z=5+2t\end{matrix}\right.\)
Tọa độ hình chiếu M' của M lên d là giao của d và (P) nên thỏa mãn:
\(4+t-2\left(1-2t\right)+2\left(5+2t\right)+6=0\) \(\Rightarrow t=-2\)
\(\Rightarrow M'\left(2;5;1\right)\)
5.
(P) nhận \(\left(2;3;1\right)\) là 1 vtpt
Gọi d là đường thẳng qua I và vuông góc (P)
\(\Rightarrow\) d nhận \(\left(2;3;1\right)\) là 1 vtcp
Phương trình tham số d: \(\left\{{}\begin{matrix}x=1+2t\\y=-2+3t\\z=1+t\end{matrix}\right.\)
H là giao điểm của d và (P) nên tọa độ thỏa mãn:
\(2\left(1+2t\right)+3\left(-2+3t\right)+1+t-11=0\) \(\Rightarrow t=1\)
\(\Rightarrow H\left(3;1;2\right)\)