Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

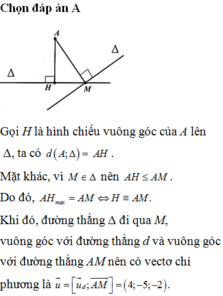
Chọn A
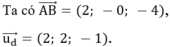
Gọi H là hình chiếu vuông góc của B lên Δ, lúc đó d(B, Δ) = BH ≤ BA
Do đó d(B, Δ) lớn nhất khi H ≡ A ![]()

Đáp án B.
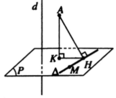
Gọi (P) là mặt phẳng qua M và vuông góc với d.Phương trình của ![]()
Gọi H,K lần lượt là hình chiếu vuông góc cùa A trên ∆,(P)
Ta có: K(-3;-2;-1), ![]()
Vậy khoảng cách từ A đến bé nhất khi A đi qua M,K.
∆ có vectơ chỉ phương ![]()

Chọn A
Gọi H là hình chiếu vuông góc của A lên Δ, ta có d (A; Δ) = AH.
Mặt khác, vì M ∈ Δ nên AH ≤ AM. Do đó, 
Khi đó, đường thẳng Δ đi qua M, vuông góc với đường thẳng d và vuông góc với đường thẳng AM nên có véctơ chỉ phương là ![]()

Chọn C
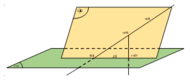
Ta có mặt phẳng α nhận vectơ n α → = ( 1 ; 1 ; 1 ) là vectơ pháp tuyến, đường thẳng d đi qua điểm A(0;-1;2) và nhận u d → = ( 1 ; 2 ; - 1 ) là vectơ chỉ phương.
Gọi β là mặt phẳng chứa đường thẳng d và vuông góc với mặt phẳng α
![]()
Khi đó đường thẳng ∆ là giao tuyến của hai mặt phẳng α và β . Do đó một vectơ chỉ phương của đường thẳng ∆ là .
![]()
Mà u → = ( 1 ; a ; b ) nên a=4, b = -5 => a+b = 4-5 =-1.


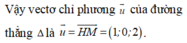


Đáp án A.
Gọi u → = ( a ; b ; c ) là vecto chỉ phương của đường thẳng ∆
Vì ∆ ⊥ d
Khoảng cách từ điểm B đến đường thẳng ∆ là
Mặt khác c = 2a + 2b
Dấu bằng xảy ra
Vậy u → = ( 4 ; - 3 ; 2 )