Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do phương trình tổng quát mặt phẳng x a + y b + z c = 1 với a = b = c . Biện luận theo dấu của a, b, c ta nhận được 3 mặt.
Đáp án cần chọn là A

Đáp án A
Gọi pt mặt phẳng cần tìm là:
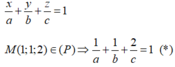
![]()
![]()
![]()
Thay vào (*) ta thấy chỉ có 3 bộ thỏa mãn: ![]() tương ứng có 3 mặt phẳng thỏa mãn đề bài.
tương ứng có 3 mặt phẳng thỏa mãn đề bài.

Đáp án C.
Đặt A = a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c a b c ≠ 0
Ta có H A → = a − 1 ; − 2 ; − 3 , H B → = − 1 ; b − 2 ; − 3 , B C → = 0 ; − b ; c , A C → = − a ; 0 ; c
H là trực tâm Δ A B C ⇒ H A → . B C → = 0 H B → . A C → = 0 ⇔ 2 b − 3 c = 0 a − 3 c = 0 .
Phương trình mặt phẳng có dạng x a + y b + z c = 1
⇔ x a + y a 2 + z a 3 = 1 ⇔ x + 2 y + 3 z − a = 0
Vì A B C đi qua H ⇒ 1 + 2.2 + 3.3 = a ⇔ a = 14
Vậy phương trình (P) là x + 2 y + 3 z − 14 = 0 .

Gọi A(a;0;0), B(0;b;0), C(0;0;c) có ![]() và
và ![]()
Vì O.ABC là hình chóp đều nên
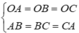
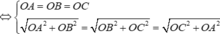
⇔ O A = O B = O C > 0
Do đó với O A = O B = O C ⇔ a = b = c
Vậy ta có hệ điều kiện:
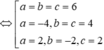
Vậy ta có ba mặt phẳng thoả mãn là
x+y=z-6=0; x-y-z+4=0; x-y+z-2=0
Vì vậy ![]()
Chọn đáp án D.

Đáp án D.
Phương pháp: Gọi A(a;0;0), B(0;b;0), C(0;0;c) => |a| = |b| = |c|, chia các trường hợp để phá trị tuyệt đối và viết phương trình mặt phẳng (P) dạng đoạn chắn.
Cách giải: Giả sử A(a;0;0), B(0;b;0), C(0;0;c) ta có: OA = |a|; OB = |b|; OC = |c|
OA = OB = OC ≠ 0 ó |a| = |b| = |c| ≠ 0
TH1: 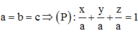
![]()
![]()
![]()
TH2: 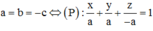
![]()
![]()
![]()
TH3: 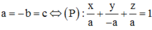
![]()
![]()
![]()
TH4: ![]()
![]()
![]()
![]()
Vậy có 4 mặt phẳng thỏa mãn yêu cầu bài toán

Chọn đáp án A.




Suy ra số tập hợp con khác rỗng của S là 2 3 - 1 = 7

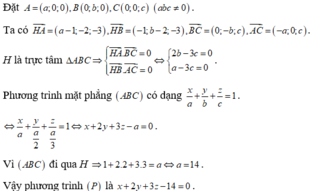


Đáp án D