Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Do phương trình tổng quát mặt phẳng x a + y b + z c = 1 với a = b = c . Biện luận theo dấu của a, b, c ta nhận được 3 mặt.
Đáp án cần chọn là A

Đáp án A
Gọi pt mặt phẳng cần tìm là: x a + y b + z c = 1 M ( 1 ; 1 ; 2 ) ∈ ( P ) ⇒ 1 a + 1 b + 2 c = 1 ( * ) A ( a ; 0 ; 0 ) , B ( 0 ; b ; 0 ) , C ( 0 ; 0 ; c ) : O A = O B = O C ⇒ a = b = c = α > 0 ⇒ ( a ; b ; c ) ∈ { ( α ; α ; α ) , ( − α ; α ; α ) , ( α ; − α ; α ) , ( α ; α ; − α ) , ( − α ; − α ; α ) , ( − α ; α ; − α ) , ( α ; − α ; − α ) , ( − α ; − α ; − α ) }
Thay vào (*) ta thấy chỉ có 3 bộ thỏa mãn: ( α ; α ; α ) , ( − α ; α ; α ) , ( α ; − α ; α ) tương ứng có 3 mặt phẳng thỏa mãn đề bài

Đáp án A.
Phương trình mặt phẳng (P) có dạng
x a + y b + z c = 1 ,
với A a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c .
Ta có O A = O B = O C ⇔ a = b = c
và M ∈ P ⇒ 1 a + 1 b + 2 c = 1 ( * )
Suy ra a = b = c a = − b = c và a = b = − c a = − b = − c ,
a = b = − c không thỏa mãn điều kiện (*)
Vậy có 3 mặt phẳng thỏa mãn yêu cầu bài toán.

Đáp án C.
Đặt A = a ; 0 ; 0 , B 0 ; b ; 0 , C 0 ; 0 ; c a b c ≠ 0
Ta có H A → = a − 1 ; − 2 ; − 3 , H B → = − 1 ; b − 2 ; − 3 , B C → = 0 ; − b ; c , A C → = − a ; 0 ; c
H là trực tâm Δ A B C ⇒ H A → . B C → = 0 H B → . A C → = 0 ⇔ 2 b − 3 c = 0 a − 3 c = 0 .
Phương trình mặt phẳng có dạng x a + y b + z c = 1
⇔ x a + y a 2 + z a 3 = 1 ⇔ x + 2 y + 3 z − a = 0
Vì A B C đi qua H ⇒ 1 + 2.2 + 3.3 = a ⇔ a = 14
Vậy phương trình (P) là x + 2 y + 3 z − 14 = 0 .


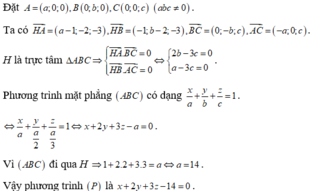


Đáp án A
Gọi pt mặt phẳng cần tìm là:
Thay vào (*) ta thấy chỉ có 3 bộ thỏa mãn: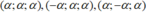 tương ứng có 3 mặt phẳng thỏa mãn đề bài.
tương ứng có 3 mặt phẳng thỏa mãn đề bài.