Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

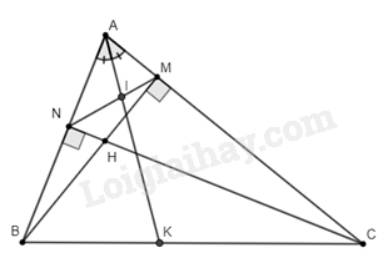
a) Vì \(BM\)là đường cao nên \(\widehat {AMB} = 90^\circ \); vì \(CN\)là đường cao nên \(\widehat {ANC} = 90^\circ \)
Xét tam giác \(AMB\) và tam giác \(ANC\) có:
\(\widehat A\) (chung)
\(\widehat {ANB} = \widehat {ANC} = 90^\circ \) (chứng minh trên)
Suy ra, \(\Delta AMB\backsim\Delta ANC\) (g.g).
Suy ra, \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Do đó, \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (tỉ lệ thức)
Xét tam giác \(AMN\) và tam giác \(ABC\) có:
\(\widehat A\) (chung)
\(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}}\) (chứng minh trên)
Suy ra, \(\Delta AMN\backsim\Delta ABC\) (c.g.c).
b) Xét tam giác \(AMN\) có \(AI\) là đường phân giác của \(\widehat {MAN}\left( {I \in MN} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{IM}}{{IN}} = \frac{{AM}}{{AN}}\)
Xét tam giác \(ABC\) có \(AK\) là đường phân giác của \(\widehat {BAC}\left( {K \in BC} \right)\).
Theo tính chất đường phân giác ta có:
\(\frac{{BK}}{{KC}} = \frac{{AB}}{{AC}}\)
Mà \(\frac{{AM}}{{AN}} = \frac{{AB}}{{AC}}\) (chứng minh trên) nên \(\frac{{IM}}{{IN}} = \frac{{KB}}{{KC}}\) (điều phải chứng minh).

a) Ta có: \(\Delta ABC \backsim \Delta MNP\) suy ra \(\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}}\,\,\left( 1 \right)\) và \(\widehat B = \widehat N\)
Mà D là trung điểm BC và Q là trung điểm NP nên \(BC = 2BD\) và \(NP = 2NQ\)
Thay vào biểu thức (1) ta được \(\frac{{AB}}{{MN}} = \frac{{2BD}}{{2NQ}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\)
Xét tam giác ABD và tam giác MNQ có:
\(\frac{{AB}}{{MN}} = \frac{{BD}}{{NQ}}\) và \(\widehat B = \widehat N\)
\( \Rightarrow \Delta ABD \backsim \Delta MNQ\) (c-g-c)
b) Vì \(\Delta ABD \backsim \Delta MNQ\) nên ta có \(\frac{{AB}}{{MN}} = \frac{{AD}}{{MQ}}\,\,\left( 2 \right)\) và \(\widehat {BAD} = \widehat {NMQ}\) hay \(\widehat {BAG} = \widehat {NMK}\)
Mà G và K lần lượt là trọng tâm của tam giác ABC và tam giác MNP nên \(AD = \frac{3}{2}AG\) và \(MQ = \frac{3}{2}MK\).
Thay vào (2) ta được: \(\frac{{AB}}{{MN}} = \frac{{\frac{3}{2}AG}}{{\frac{3}{2}MK}} \Rightarrow \frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\)
Xét tam giác ABG và tam giác NMK có:
\(\frac{{AB}}{{MN}} = \frac{{AG}}{{MK}}\) và \(\widehat {BAG} = \widehat {NMK}\)
\( \Rightarrow \)\(\Delta ABG \backsim \Delta MNK\) (c-g-c)

a) Nếu \(\Delta A'B'C' = \Delta ABC\) thì tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Vì hai tam giác bằng nhau có các góc tương ứng bằng nhau và các cạnh tương ứng bằng nhau.
Khi đó, \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = 1\end{array} \right.\). Vậy \(\Delta A'B'C'\backsim\Delta ABC\) và tỉ số đồng dạng là 1.
b) Vì \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số đồng dạng là \(k\) nên tỉ số đồng dạng là: \(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\).
Khi đó, \(\Delta ABC\backsim\Delta A'B'C'\) đồng dạng với tỉ số đồng dạng là: \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = \frac{{BC}}{{B'C'}} = \frac{1}{k}\).
Vậy \(\Delta ABC\backsim\Delta A'B'C'\)theo tỉ số \(\frac{1}{k}\).

a) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = k;\,\,\widehat B = \widehat {B'}\)
Mà AM và A’M’ lần lượt là trung tuyến của hai tam giác ABC và A’B’C’ nên M và M’ lần lượt là trung điểm của BC và B’C’.
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}BC;\,\,B'M' = \frac{1}{2}B'C'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}} = k\end{array}\)
Xét tam giác ABM và tam giác A’B’M’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABM \backsim \Delta A'B'M'\) (c-g-c)
\( \Rightarrow \frac{{AM}}{{A'M'}} = \frac{{BM}}{{B'M'}} = k\)
b) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = k;\,\,\widehat B = \widehat {B'}\)
\(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Vì AD và A’D’ lần lượt là phân giác của tam giác ABC và tam giác A’B’C’ nên ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) và \(\frac{{D'B'}}{{D'C'}} = \frac{{A'B'}}{{A'C'}}\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{D'B'}}{{D'C'}} \Rightarrow \frac{{DB}}{{D'B'}} = \frac{{DC}}{{D'C'}} = \frac{{DB + DC}}{{D'B' + D'C'}} = \frac{{BC}}{{B'C'}}\)
Mà \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (chứng minh ở câu a) nên \(\frac{{DB}}{{D'B'}} = \frac{{AB}}{{A'B'}}\)
Xét tam giác ABD và tam giác A’B’D’ có:
\(\frac{{BD}}{{B'D'}} = \frac{{AB}}{{A'B'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABD \backsim \Delta A'B'D'\) (c-g-c)
\( \Rightarrow \frac{{AD}}{{A'D'}} = \frac{{AB}}{{A'B'}} = k\)
c) Ta có \(\widehat B = \widehat {B'}\) và \(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
\( \Rightarrow \Delta ABH \backsim \Delta A'B'H'\) (g-g)
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AH}}{{A'H'}} = k\)

Vì \(\Delta ADE\backsim\Delta AMN\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}}\end{array} \right.\)
Vì \(DE\) là đường trung bình của tam giác \(AMN\)nên \(DE = \frac{1}{2}MN\)
\( \Rightarrow \left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {ADE} = \widehat {AMN};\widehat {AED} = \widehat {ANM}\\\frac{{AD}}{{AM}} = \frac{{AE}}{{AN}} = \frac{{DE}}{{MN}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AM = 2AD;AN = 2AE;MN = 2DE\)
Lại có, \(\Delta AMN\backsim\Delta ABC\) nên \(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array} \right.\)
Vì \(MN\) là đường trung bình của tam giác \(ABC\)nên \(MN = \frac{1}{2}BC\)
\(\left\{ \begin{array}{l}\widehat A = \widehat A;\widehat {AMN} = \widehat {ABC};\widehat {ANM} = \widehat {ACB}\\\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}} = \frac{1}{2}\end{array} \right.\)
\( \Rightarrow AB = 2AM;AC = 2AN;BC = 2MN\)
Vì tam giác \(\Delta ADE\backsim\Delta AMN,\Delta AMN\backsim\Delta ABC,\) nên \(\Delta ADE\backsim\Delta ABC\)
Tỉ số đồng dạng là: \(\frac{{AD}}{{AB}} = \frac{{\frac{{AM}}{2}}}{{2AM}} = \frac{1}{4}\).
Vậy tỉ số đồng dạng là \(\frac{1}{4}\).

a) Ta có \(\Delta ABC\backsim\Delta DEF\) theo tỉ số đồng dạng \(k = \frac{2}{5}\) nên
\(\frac{{AB}}{{DE}} = \frac{{AC}}{{DF}} = \frac{{BC}}{{EF}} = \frac{2}{5} \Rightarrow AB = \frac{2}{5}DE;AC = \frac{2}{5}DF;BC = \frac{2}{5}EF\).
Chu vi tam giác \(ABC\) là:
\({C_{ABC}} = AB + AC + BC\) (đơn vị độ dài).
Chu vi tam giác \(DEF\) là:
\({C_{DEF}} = DE + DF + EF\)
Tỉ số chu vi của \(\Delta ABC\) và \(\Delta DEF\) là:
\(\frac{{{C_{ABC}}}}{{{C_{DEF}}}} = \frac{{AB + AC + BC}}{{DE + DF + EF}} = \frac{{\frac{2}{5}DE + \frac{2}{5}DF + \frac{2}{5}EF}}{{DE + DF + EF}} = \frac{{\frac{2}{5}\left( {DE + DF + EF} \right)}}{{DE + DF + EF}} = \frac{2}{5}\).
b) Chu vi tam giác \(ABC\) là:
\(36:\left( {5 - 2} \right).2 = 24\left( {cm} \right)\)
Chu vi tam giác \(DEF\) là:
\(36:\left( {5 - 2} \right).5 = 60\left( {cm} \right)\)
Vậy chu vi tam giác \(ABC\) là 24cm; chu vi tam giác \(DEF\) là 60cm.

Đáp án đúng là A
Vì \(\Delta ABC\backsim\Delta MNP\) theo tỉ số \(k = 3\) nên \(\Delta MNP\backsim\Delta ABC\) theo tỉ số \(\frac{1}{3}\).

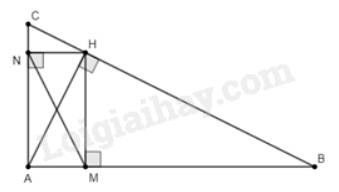
a) Xét \(\Delta AMH\) và \(\Delta AHB\) có:
\(\widehat {HAM}\) chung (do \(\widehat {HAM}\) cũng là \(\widehat {HAB}\))
\(\widehat {AMH} = \widehat {AHB} = 90^\circ \) (do \(HM \bot AB\) và \(AH\) là đường cao)
Do đó, \(\Delta AMH\backsim\Delta AHB\) (g.g).
b) Vì \(\Delta AMH\backsim\Delta AHB\) nên \(\frac{{AM}}{{AH}} = \frac{{AH}}{{AB}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra \(AM.AB = A{H^2}\) (1)
- Xét \(\Delta ANH\) và \(\Delta AHC\) có:
\(\widehat {HAN}\) chung (do \(\widehat {HAN}\) cũng là \(\widehat {HAC}\))
\(\widehat {ANH} = \widehat {AHC} = 90^\circ \) (do \(HN \bot AC\) và \(AH\) là đường cao)
Do đó, \(\Delta ANH\backsim\Delta AHC\) (g.g).
Vì \(\Delta ANH\backsim\Delta AHC\) nên \(\frac{{AN}}{{AH}} = \frac{{AH}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Suy ra \(AN.AC = A{H^2}\) (2)
Từ (1) và (2) suy ra, \(AM.AB = AN.AC\)(điều phải chứng minh).
c) Từ câu b ta có:
\(AM.AB = AN.AC \Rightarrow \frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\) (tỉ lệ thức)
Xét \(\Delta ANM\)và \(\Delta ABC\) ta có:
\(\widehat A\) chung
\(\frac{{AM}}{{AC}} = \frac{{AN}}{{AB}}\) (chứng minh trên)
Do đó, \(\Delta ANM\backsim\Delta ABC\)(c.g.c)
d) Áp dụng định lí Py- ta – go cho tam giác \(ABC\) vuông tại \(A\) ta có:
\(B{C^2} = A{B^2} + A{C^2} = {9^2} + {12^2} = 225 \Rightarrow BC = 15cm\)
Diện tích tam giác \(ABC\) là: \({S_{\Delta ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}AH.BC\)
\( \Rightarrow AH.BC = AB.AC\)
\( \Rightarrow AH = \frac{{AB.AC}}{{BC}} = \frac{{9.12}}{{15}} = 7,2cm\).
Ta có: \(A{H^2} = AM.AB = AM.9 = 7,{2^2} \Rightarrow AM = \frac{{7,{2^2}}}{9} = 5,76cm\)
\(A{H^2} = AN.AC = AN.12 = 7,{2^2} \Rightarrow AN = \frac{{7,{2^2}}}{{12}}4,32cm\).
Diện tích tam giác vuông \(AMN\) là:
\({S_{AMN}} = \frac{1}{2}AM.AN = \frac{1}{2}.5,76.4,32 = 12,4416c{m^2}\).
Vậy diện tích tam giác \(AMN\) là 12,4416cm2.
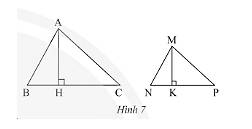
a) Vì tam giác \(\Delta MNP\backsim\Delta ABC\) nên \(\widehat B = \widehat N\) (hai góc tương ứng).
Vì \(MK\) là đường cao nên \(\widehat {MKN} = 90^\circ \);Vì \(AH\) là đường cao nên \(\widehat {AHB} = 90^\circ \)
Xét \(\Delta MNK\) và \(\Delta ABH\) có:
\(\widehat B = \widehat N\) (chứng minh trên)
\(\widehat {MKN} = \widehat {AHB} = 90^\circ \)
Do đó, \(\Delta MNK\backsim\Delta ABH\) (g.g)
Vì \(\Delta MNK\backsim\Delta ABH\) nên ta có: \(\frac{{MN}}{{AB}} = \frac{{NK}}{{BH}} = \frac{{MK}}{{AH}} = k \Rightarrow \frac{{MK}}{{AH}} = k\).
b) Vì \(\Delta MNP\backsim\Delta ABC\) nên \(\frac{{MN}}{{AB}} = \frac{{NP}}{{BC}} = \frac{{MP}}{{AC}} = k\)
\( \Rightarrow \frac{{NP}}{{BC}} = k \Leftrightarrow NP = kBC\)
Vì \(\frac{{MK}}{{AH}} = k \Rightarrow MK = kAH\)
Diện tích tam giác \(MNP\) là:
\({S_1} = \frac{1}{2}.MK.NP\) (đvdt)
Diện tích tam giác \(ABC\) là:
\({S_2} = \frac{1}{2}.AH.BC\) (đvdt)
Ta có: \(\frac{{{S_1}}}{{{S_2}}} = \frac{{\frac{1}{2}.MK.NP}}{{\frac{1}{2}.AH.BC}} = \frac{{kAH.kBC}}{{AH.BC}} = {k^2}\) (điều phải chứng minh)