Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Vì ΔA′B′C′ ∽ ΔABC
=> \(\widehat B = \widehat {B'};\frac{{A'H'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\)
Xét hai tam giác vuông A'H'B' (vuông tại H') và tam giác vuông AHB (vuông tại H), có:
\(\widehat B = \widehat {B'}\)
=> ΔA′H′B′ ∽ ΔAHB
=> \(\frac{{A'H'}}{{AH}} = \frac{{A'B'}}{{AB}}\)
Mà \(\frac{{A'B'}}{{AB}} = k\)
=> \(\frac{{A'H'}}{{AH}} = k\)
b) Có diện tích tam giác ABC là: \(\frac{1}{2}\)AH.BC
Có diện tích tam giác A'B'C' là: \(\frac{1}{2}\)A′H′.B′C′
Xét tỉ lệ giữa hai tam giác A'B'C' và tam giác ABC có:
\(\frac{{\frac{1}{2}A'H'.B'C'}}{{\frac{1}{2}AH.BC}} = \frac{{A'H'}}{{AH}}.\frac{{B'C'}}{{BC}} = k.k = {k^2}\)

Vì ΔA’B’C’ ∽ ΔABC
=> ΔA’M’B’ ∽ ΔAMB
=> \(\frac{{A'M'}}{{AM}} = \frac{{A'B'}}{{AB}}(1)\) (1)
Vì \(\Delta A'B'C'\) ∽ ΔABC
=> Vì ΔA′B′N′ ∽ ΔABN
=> \(\frac{{B'N'}}{{BN}} = \frac{{A'B'}}{{AB}}\) (2)
Từ (1) và (2) => \(\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}}\)(3)
Vì ΔA’B’C’ ∽ ΔABC
=> Vì ΔA’C’P’ ∽ ΔACP
=> \(\frac{{C'P'}}{{CP}} = \frac{{A'C'}}{{AC}}\) (4)
Vì ΔA′B′C′ ∽ ΔABC
=> ΔA′M′C′ ∽ ΔAMC
=> \(\frac{{A'M'}}{{AM}} = \frac{{A'C'}}{{AC}}\) (5)
Từ (4) và (5) => \(\frac{{C'P'}}{{CP}} = \frac{{A'M'}}{{AM}}\) (6)
Từ (3) và (6) => \(\frac{{A'M'}}{{AM}} = \frac{{B'N'}}{{BN}} = \frac{{C'P'}}{{CP}}\)

\(\dfrac{B'A}{B'C}=\dfrac{S_{AMB'}}{S_{CMB'}}=\dfrac{S_{ABB'}}{S_{CBB'}}=\dfrac{S_{ABB'}-S_{AMB'}}{S_{CBB'}-S_{CMB'}}=\dfrac{S_{ABM}}{S_{CBM}}\)
\(\dfrac{C'A}{C'B}=\dfrac{S_{AMC'}}{S_{BMC'}}=\dfrac{S_{ACC'}}{S_{BCC'}}=\dfrac{S_{ACC'}-S_{AMC'}}{S_{BCC'}-S_{BMC'}}=\dfrac{S_{ACM}}{S_{CBM}}\)
\(\dfrac{MA}{MA'}=\dfrac{S_{ABM}}{S_{A'BM}}=\dfrac{S_{ACM}}{S_{A'CM}}=\dfrac{S_{ABM}+S_{ACM}}{S_{A'BM}+S_{A'CM}}=\dfrac{S_{ABM}+S_{ACM}}{S_{MBC}}=\dfrac{S_{ABM}}{S_{MBC}}+\dfrac{S_{ACM}}{S_{MBC}}=\dfrac{B'A}{B'C}+\dfrac{C'A}{C'B}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{A'B'}{3}=\dfrac{B'C'}{14}=\dfrac{C'A'}{13}=\dfrac{A'B'+B'C'+C'A'}{3+14+13}=\dfrac{90}{30}=3\)
Do đó: A'B'=9cm; B'C'=42cm; C'A'=39cm

Vì A’, B’, C’ lần lượt là trung điểm của AG, BG, CG nên A’B’, B’C’, A’C’ lần lượt là đường trung bình của các tam giác AGB, BGC, AGC.
Khi đó: \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{2}\)
Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}} = \frac{1}{2}\)
Vậy \(\Delta A'B'C' \backsim\Delta ABC\) (c-c-c)

Theo giả thiết, ta có:
\(\Delta ABC \backsim\Delta MNP\) theo hệ số tỉ lệ là \(\frac{1}{{1\,000\,000}}\)
\(\Delta A'B'C' \backsim\Delta MNP\) theo hệ số tỉ lệ là \(\frac{1}{{1\,500\,000}}\).
Từ đó ta có:
\(\begin{array}{l}\frac{{AB}}{{MN}} = \frac{{BC}}{{NP}} = \frac{{CA}}{{PM}} = 1\,000\,000\\ \Rightarrow AB = 1\,000\,000MN,\,\,BC = 1\,000\,000NP,\,\,CA = 1\,000\,000PM\end{array}\)
và \(\begin{array}{l}\frac{{A'B'}}{{MN}} = \frac{{B'C'}}{{NP}} = \frac{{C'A'}}{{PM}} = 1\,500\,000\\ \Rightarrow A'B' = 1\,500\,000MN,\,\,B'C' = 1\,500\,000NP,\,\,C'A' = 1\,500\,000PM\end{array}\)
Ta thấy
\(\begin{array}{l}\frac{{AB}}{{A'B'}} = \frac{{1\,000\,000MN}}{{1\,500\,000MN}} = \frac{2}{3}\\\frac{{BC}}{{B'C'}} = \frac{{1\,000\,000NP}}{{1\,500\,000NP}} = \frac{2}{3}\\\frac{{CA}}{{C'A'}} = \frac{{1\,000\,000PM}}{{1\,500\,000PM}} = \frac{2}{3}\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = \frac{{CA}}{{C'A'}}\end{array}\)
\( \Rightarrow \Delta ABC \backsim\Delta A'B'C'\) (c-c-c) với tỉ số đồng dạng là \(\frac{2}{3}\).

Xét tam giác A’B’C’ và tam giác ABC có:
\(\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}}\) và \(\widehat {A'} = \widehat A = 90^\circ \)
\( \Rightarrow \Delta A'B'C' \backsim \Delta ABC\) (c-g-c)
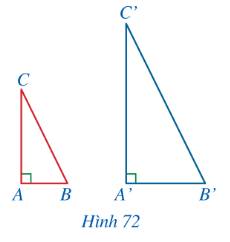
a) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}} = k;\,\,\widehat B = \widehat {B'}\)
Mà AM và A’M’ lần lượt là trung tuyến của hai tam giác ABC và A’B’C’ nên M và M’ lần lượt là trung điểm của BC và B’C’.
\(\begin{array}{l} \Rightarrow BM = \frac{1}{2}BC;\,\,B'M' = \frac{1}{2}B'C'\\ \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}} = k\end{array}\)
Xét tam giác ABM và tam giác A’B’M’ có:
\(\frac{{AB}}{{A'B'}} = \frac{{BM}}{{B'M'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABM \backsim \Delta A'B'M'\) (c-g-c)
\( \Rightarrow \frac{{AM}}{{A'M'}} = \frac{{BM}}{{B'M'}} = k\)
b) Vì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số đồng dạng \(k\) nên \(\frac{{AB}}{{A'B'}} = \frac{{AC}}{{A'C'}} = k;\,\,\widehat B = \widehat {B'}\)
\(\frac{{AB}}{{AC}} = \frac{{A'B'}}{{A'C'}}\)
Vì AD và A’D’ lần lượt là phân giác của tam giác ABC và tam giác A’B’C’ nên ta có \(\frac{{DB}}{{DC}} = \frac{{AB}}{{AC}}\) và \(\frac{{D'B'}}{{D'C'}} = \frac{{A'B'}}{{A'C'}}\)
\( \Rightarrow \frac{{DB}}{{DC}} = \frac{{D'B'}}{{D'C'}} \Rightarrow \frac{{DB}}{{D'B'}} = \frac{{DC}}{{D'C'}} = \frac{{DB + DC}}{{D'B' + D'C'}} = \frac{{BC}}{{B'C'}}\)
Mà \(\frac{{AB}}{{A'B'}} = \frac{{BC}}{{B'C'}}\) (chứng minh ở câu a) nên \(\frac{{DB}}{{D'B'}} = \frac{{AB}}{{A'B'}}\)
Xét tam giác ABD và tam giác A’B’D’ có:
\(\frac{{BD}}{{B'D'}} = \frac{{AB}}{{A'B'}}\) và \(\widehat B = \widehat {B'}\)
\( \Rightarrow \Delta ABD \backsim \Delta A'B'D'\) (c-g-c)
\( \Rightarrow \frac{{AD}}{{A'D'}} = \frac{{AB}}{{A'B'}} = k\)
c) Ta có \(\widehat B = \widehat {B'}\) và \(\widehat {AHB} = \widehat {A'H'B'} = 90^\circ \)
\( \Rightarrow \Delta ABH \backsim \Delta A'B'H'\) (g-g)
\( \Rightarrow \frac{{AB}}{{A'B'}} = \frac{{AH}}{{A'H'}} = k\)