Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

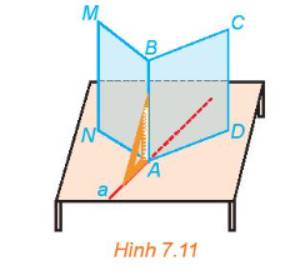
a) Theo tài liệu nói trên, góc xOy trong hình nên có số đo từ 100° đến 105°
b) Vì các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế nên góc giữa lưng ghế và mặt ghế là góc giữa Ox và Oy mà góc xOy có số đo từ 100° đến 105°
Do đó nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo 750 đến 800

Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng ( u n ) có u 1 = 7 , d = 5.
Gọi n là số ô trên bàn cờ thì u 1 + u 2 + ⋯ + u n = 25450 = S n .
Ta có 25450 = S n = n u 1 + n n − 1 2 d = 7 n + n 2 − n 2 .5
⇔ 5 n 2 + 9 n − 50900 = 0 ⇔ n = 100
Chọn đáp án B

Chọn D.
Số hạt dẻ trên mỗi ô (bắt đầu từ ô thứ nhất) theo thứ tự đó lập thành cấp số cộng có u1 = 7; d = 5 .
Gọi n là số ô trên bàn cờ thì u1 + u2 + L + un = 25450 = Sn
Ta có 25450 = Sn = ![]() 5n2 + 9n – 50900 = 0
5n2 + 9n – 50900 = 0
Hay n = 100.

Số hạt thóc ở các ô từ ô thứ nhất đến thứ sáu: 1; 2; 4; 8; 16; 32

tham khảo:
Do các hình vuông được cắt ra từ tấm tôn góc ban đầu có kích thước giống nhau, do đó khi ghép các mép lại với nhau, ta sẽ có được đường biên của chiếc hộp chữ nhật. Các cạnh của hình vuông trùng với các cạnh của hộp chữ nhật, do đó khi các mặt được ghép lại với nhau, chúng sẽ tạo thành các mặt của hộp chữ nhật. Vì vậy, bằng cách này, bác Hùng đã tạo ra một chiếc thùng hình hộp chữ nhật từ một tấm tôn hình chữ nhật ban đầu.

Do mặt bàn và mặt đất không có điểm chung nên chúng song song với nhau.

Đáp án D
Gọi ô chứa hạt thóc thỏa mãn đề bài là ô thứ n ( n ∈ N , n > 1 ) . Khi đó




tick cho mình đi
Giả sử có ít nhất 7 ô mà số khăn ăn phủ lên nó là số lẻ. Khi đó, tổng số khăn ăn phủ lên bàn ăn là 7l, với l là số lẻ.
Ta có thể chia bàn ăn thành 8 ô hàng ngang và 8 ô hàng dọc. Do đó, tổng số khăn ăn phủ lên bàn ăn cũng phải chia hết cho 8.
Tuy nhiên, 7l không chia hết cho 8 với mọi giá trị của l. Do đó, giả thuyết của chúng ta là sai.
Vậy, có ít nhất 1 ô mà số khăn ăn phủ lên nó là số chẵn.
Chứng minh bằng phản chứng. Giả sử không có ô nào mà số khăn ăn phủ lên nó là số chẵn. Khi đó, số khăn ăn phủ lên mỗi ô là 1 hoặc 3.
Do đó, tổng số khăn ăn phủ lên bàn ăn là 2n, với n là số ô.
Ta có thể chia bàn ăn thành 8 ô hàng ngang và 8 ô hàng dọc. Do đó, tổng số khăn ăn phủ lên bàn ăn cũng phải chia hết cho 8.
Tuy nhiên, 2n không chia hết cho 8 với mọi giá trị của n. Do đó, giả thuyết của chúng ta là sai.
Vậy, có ít nhất 1 ô mà số khăn ăn phủ lên nó là số chẵn.
Kết luận: Cho dù có đặt khăn ăn như thế nào thì cũng luôn tồn tại ít nhất 1 ô mà số khăn ăn phủ lên nó là một số chẵn.
share Google it