Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \({u_1} = 15,\;d = 3\)
\({S_n} = \frac{n}{2}\left[ {2 \times 15 + \left( {n - 1} \right) \times 3} \right] = 870\)
\(\frac{n}{2}\left( {27 + 3n} \right) = 870\)
\(\begin{array}{l} \Leftrightarrow 3{n^2} + 27n - 1740 = 0\\ \Leftrightarrow \left[ \begin{array}{l}n = 20\\n = - 29(L)\end{array} \right.\end{array}\)
Vậy cần phải thiết kế 20 hàng ghế.

Chọn B.
Giả sử số thứ tự trong danh sách là ![]()
Do dãy này là cấp số cộng nên ta có ![]()
![]()
Số phần tử của không gian mẫu là ![]()
Gọi A là biến cố “Tổng các số thứ tự của hai em ngồi đối diện nhau là bằng nhau”. Để biến cố này xảy ra ta thực hiện liên tiếp các bước sau:
Bước 1: xếp thứ tự cặp học sinh có các cặp số thứ tự là ![]()
![]()
vào trước cặp ghế đối diện nhau. Bước này có 5! cách.
Bước 2: xếp từng cặp một ngồi vào cặp ghế đối diện đã ) Chọn ở bước . Bước này có 2 5 cách.
Suy ra số kết quả thuận lợi cho biến cố A là ![]()
Vậy xác suất của biến cố A là ![]()

Theo đề bài ta có dãy số chỉ số ghế có ở các hàng là một cấp số cộng có số hạng đầu \({u_1} = 17\) và công sai \(d = 3\).
a) Số ghế có ở hàng cuối cùng là: \({u_{20}} = {u_1} + 19{\rm{d}} = 17 + 19.3 = 74\) (ghế).
b) Tổng số ghế có trong rạp là: \({S_{20}} = \frac{{20\left[ {2{u_1} + 19{\rm{d}}} \right]}}{2} = \frac{{20\left[ {2.17 + 19.3} \right]}}{2} = 910\) (ghế).

Đáp án A
Số cách xếp tuỳ ý là 45!.
Ta tìm số cách xếp thoả mãn; giả sử số ghế của A,B,C lần lượt là a,b,c.
Theo giả thiết có
![]()
Do đó b,c phải cùng chẵn hoặc cùng lẻ.
Nếu b,c chẵn có A 22 2 cách xếp B,C;
1 cách xếp A và 42! cách xếp học sinh khác.
Nếu b,c lẻ có A 23 2 cách xếp B, C;
1 cách xếp A và 42! cách xếp học sinh khác.
Số cách xếp thoả mãn là 42 ! ( A 22 2 + A 23 2 )
Vậy xác suất cần tính
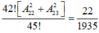

a: Có thể xác định được bằng cách bằng cách sử dụng góc giữa hai cây chống vuông góc với mỗi cánh.
b: Góc giữa hai mặt phẳng là góc giữa hai đường thẳng lần lượt vuông góc với hai mặt phẳng đó
Khi đặt thiết bị lên mp nghiêng (Q) thì ta sẽ có:
\(OM\perp\left(Q\right);ON\perp\left(P\right)\)
\(OM\subset\left(P\right),ON\subset\left(Q\right)\)
=>\(\widehat{\left(P\right),\left(Q\right)}=\widehat{\left(OM;ON\right)}=\widehat{MON}=90^0\)

a) Có 2 cách xếp.
Bạn A có 6! cách.
Bạn B có 6! cách.
Đổi vị trí A,B có tất cả 2*(6!)2 cách xếp chỗ.
b) Chọn 1 học sinh A vào vị trí bất kì: 12 cách.
Chọn 1 học sinh B đối diện A có 6 cách.
Cứ chọn liên tục như vậy ta được:
\(\left(12\cdot6\right)\cdot\left(10\cdot5\right)\cdot\left(8\cdot4\right)\cdot\left(6\cdot3\right)\cdot\left(4\cdot2\right)\cdot\left(2\cdot1\right)=2^6\cdot\left(6!\right)^2\)
cách xếp chỗ để hai bạn ngồi đối diện thì kkhasc trường nhau.





a) Theo tài liệu nói trên, góc xOy trong hình nên có số đo từ 100° đến 105°
b) Vì các tia Ox, Oy được vẽ tương ứng trên mặt ghế, lưng ghế đồng thời vuông góc với giao tuyến a của mặt ghế và lưng ghế nên góc giữa lưng ghế và mặt ghế là góc giữa Ox và Oy mà góc xOy có số đo từ 100° đến 105°
Do đó nếu thiết kế theo hướng dẫn đó thì góc giữa mặt phẳng chứa mặt ghế và mặt phẳng chứa lưng ghế có thể nhận số đo 750 đến 800