Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) AB // A’B’ \( \Rightarrow \) AB // (A’B’C’D’), AD // A’D’ \( \Rightarrow \) AD // (A’B’C’D’)
Do đó (ABCD) // (A’B’C’D’).
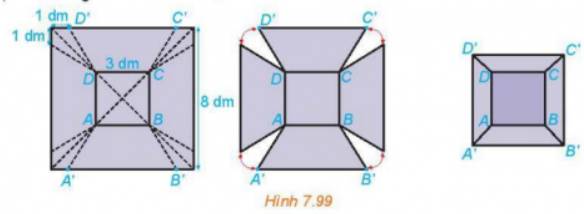
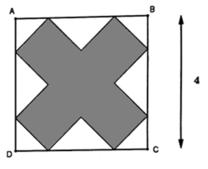
Chiếc thùng có dạng hình chóp cụt vì khi bác Hùng cắt bỏ bốn phần như nhau ở bốn góc của tấm tôn vuông, sẽ tạo thành bốn tam giác vuông cân.
Vậy chiếc thùng có dạng hình chóp cụt.
b) Cạnh bên của hình chóp cụt bằng \(\sqrt {\frac{9}{4} + \frac{{25}}{4}} = \frac{{\sqrt {34} }}{2}\left( {dm} \right)\)
c) Xét mặt chứa đường chéo của hình vuông, nó là hình thang cân có chiều cao bằng chiều cao của hình chóp cụt và được \(h = \sqrt {\frac{{34}}{4} - \frac{{18}}{4}} = 2\left( {dm} \right)\)
Thể tích cần tìm là V = 42 lít.
tham khảo:
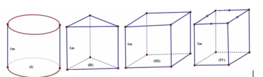
a) Hình hộp chữ nhật có 6 mặt là hình chữ nhật vì hình hộp đứng có các mặt bên là hình chữ nhật và hình hộp chữ nhật có đáy là hình chữ nhât.
b) Các đường chéo của hình hộp chữ nhật có bằng nhau và cắt nhau tại trung điểm mỗi đường. Điều này bởi vì cứ 2 đường chéo bất kì của hình hộp chữ nhật đều xác định nằm trong 1 một hình chữ nhật và là 2 đường chéo của hình chữ nhật đó.
Tham khảo
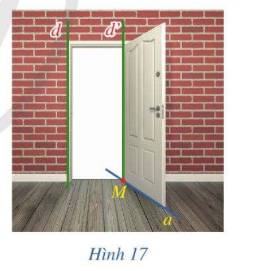
Vì sàn nhà là một mặt phẳng vuông góc với đường thẳng d. Mà đường thẳng a luôn nằm trên mặt phẳng đó nên đường thẳng d luôn vuông góc với đường thẳng a
a: \(a\perp\left(Q\right);\Delta\subset\left(Q\right)\)
=>\(\Delta\perp a\)(1)
\(b\perp\left(R\right);\Delta\subset\left(R\right)\)
=>\(\Delta\perp b\)(2)
mà a,b thuộc (P)(3)
nên từ (1), (2), (3) suy ra \(\Delta\perp\left(P\right)\)
b: Có 1 đường duy nhất
Đáp án D
Đặt x, y, h lần lượt là chiều dài, chiều rộng và chiều cao mỗi phòng.
Theo giả thiết, ta có x.3y = 1152 → y = 384 x
Để tiết kiệm chi phí nhất khi diện tích toàn phần nhỏ nhất.
Ta có 
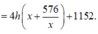
Vì h không đổi nên
S
t
p
nhỏ nhất khi 
(với x > 0) nhỏ nhất.
Khảo sát 
với x > 0 ta được f(x) nhỏ nhất khi x = 24 => y = 16
tick cho mình đi
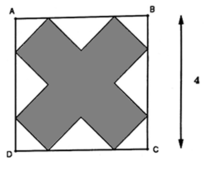
Giả sử có ít nhất 7 ô mà số khăn ăn phủ lên nó là số lẻ. Khi đó, tổng số khăn ăn phủ lên bàn ăn là 7l, với l là số lẻ.
Ta có thể chia bàn ăn thành 8 ô hàng ngang và 8 ô hàng dọc. Do đó, tổng số khăn ăn phủ lên bàn ăn cũng phải chia hết cho 8.
Tuy nhiên, 7l không chia hết cho 8 với mọi giá trị của l. Do đó, giả thuyết của chúng ta là sai.
Vậy, có ít nhất 1 ô mà số khăn ăn phủ lên nó là số chẵn.
Chứng minh bằng phản chứng. Giả sử không có ô nào mà số khăn ăn phủ lên nó là số chẵn. Khi đó, số khăn ăn phủ lên mỗi ô là 1 hoặc 3.
Do đó, tổng số khăn ăn phủ lên bàn ăn là 2n, với n là số ô.
Ta có thể chia bàn ăn thành 8 ô hàng ngang và 8 ô hàng dọc. Do đó, tổng số khăn ăn phủ lên bàn ăn cũng phải chia hết cho 8.
Tuy nhiên, 2n không chia hết cho 8 với mọi giá trị của n. Do đó, giả thuyết của chúng ta là sai.
Vậy, có ít nhất 1 ô mà số khăn ăn phủ lên nó là số chẵn.
Kết luận: Cho dù có đặt khăn ăn như thế nào thì cũng luôn tồn tại ít nhất 1 ô mà số khăn ăn phủ lên nó là một số chẵn.
share
tham khảo:
Do các hình vuông được cắt ra từ tấm tôn góc ban đầu có kích thước giống nhau, do đó khi ghép các mép lại với nhau, ta sẽ có được đường biên của chiếc hộp chữ nhật. Các cạnh của hình vuông trùng với các cạnh của hộp chữ nhật, do đó khi các mặt được ghép lại với nhau, chúng sẽ tạo thành các mặt của hộp chữ nhật. Vì vậy, bằng cách này, bác Hùng đã tạo ra một chiếc thùng hình hộp chữ nhật từ một tấm tôn hình chữ nhật ban đầu.