Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: y’= 1-e-x
Và y’= 0 khi 1-e-x = 0 nên x=0 .
Hàm số đã cho liên tục và xác định trên đoạn [-1 ;1]
Ta có: y(-1) = -1+e ; y(0) = 1 ; y(1) = 1+ e-1 .
Do đó
![]()
Vậy T= 1+ e - 1= e
Chọn B

Chọn C
Gọi A (d; e; f) thì A thuộc mặt cầu (S1): (x - 1)2 + (y - 2)2 + (z- 3)2 = 1 có tâm I1 = (1; 2; 3), bán kính R1 = 1
B (a; b; c) thì B thuộc mặt cầu (S2): (x - 3)2 + (y - 2)2 + z2 = 9 có tâm I2 = (-3; 2; 0), bán kính R2 = 3
Ta có I1I2 = 5 > R1 + R2 => (S1) và (S2) không cắt nhau và ở ngoài nhau.
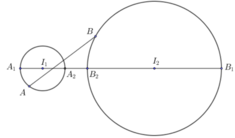
Dễ thấy F = AB, AB max khi A ≡ A1; B ≡ B1
=> Giá trị lớn nhất bằng I1I2 + R1 + R2 = 9.
AB min khi A ≡ A2; B ≡ B2
=> Giá trị nhỏ nhất bằng I1I2 - R1 - R2 = 1.
Vậy M - m =8

Ta có :
\(f'\left(x\right)=2x\ln x-x=x\left(2\ln x-1\right)=0\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\\\ln x=\frac{1}{2}\ln\sqrt{e}\end{array}\right.\)
\(\Leftrightarrow\left[\begin{array}{nghiempt}x=0\notin\left[\frac{1}{e};e^2\right]\\x=\sqrt{e}\in\left[\frac{1}{e};e^2\right]\end{array}\right.\)
Mà : \(\begin{cases}f\left(\frac{1}{e}\right)=-\frac{1}{e^2}\\f\left(e\right)=\frac{e}{2}\\f\left(e^2\right)=2e^4\end{cases}\) \(\Rightarrow\begin{cases}Max_{x\in\left[\frac{1}{e};e^2\right]}f\left(x\right)=2e^4;x=e^2\\Min_{x\in\left[\frac{1}{e};e^2\right]}f\left(x\right)=\frac{-1}{e^2};x=\frac{1}{e}\end{cases}\)

Ta có :
\(f'\left(x\right)=\frac{-\frac{\frac{1}{x}}{2\sqrt{\ln x}}}{\ln x}=-\frac{1}{2x\ln x\sqrt{\ln x}}< 0\) với mọi \(x\in\left[e;e^2\right]\Rightarrow\) hàm số nghịch biến với mọi \(x\in\left[e;e^2\right]\)
\(e\le x\le e^2\Rightarrow f\left(e\right)\ge f\left(x\right)\ge f\left(e^2\right)\Leftrightarrow1\ge f\left(x\right)\ge\frac{\sqrt{2}}{2}\)
\(\Leftrightarrow\begin{cases}Max_{x\in\left[e;e^2\right]}f\left(x\right)=1;x=e\\Min_{x\in\left[e;e^2\right]}f\left(x\right)=\frac{\sqrt{2}}{2};x=e^2\end{cases}\)
\(f\left(x\right)=\left(\ln x\right)^{-\frac{1}{2}}\Rightarrow f'\left(x\right)=-\frac{1}{2}\left(\ln x\right)^{-\frac{3}{2}}.\frac{1}{x}=-\frac{1}{2x\ln x\sqrt{\ln x}}\)
Ta có : \(\begin{cases}f\left(e\right)=1\\f\left(e^2\right)=\frac{\sqrt{2}}{2}\end{cases}\)
\(\Leftrightarrow\begin{cases}Max_{x\in\left[e;e^2\right]}f\left(x\right)=1;x=e\\Min_{x\in\left[e;e^2\right]}f\left(x\right)=\frac{\sqrt{2}}{2};x=e^2\end{cases}\)


Đáp án A
Phương pháp:
- Tìm TXĐ
- Tìm nghiệm và các điểm không xác định của y’ trên đoạn 1 2 ; e
Tính các giá trị tại 1 2 , e và các điểm vừa tìm được
- Kết luận GTLN, GTNN của hàm số từ các giá trị trên.
Cách giải:
TXĐ: D = (0;+∞)
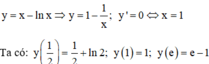
⇒ Giá trị nhỏ nhất, giá trị lớn nhất của hàm số lần lượt là: 1 và e - 1

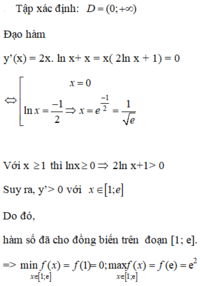
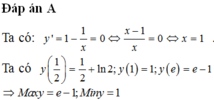
Chọn D