K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
HP
20 tháng 11 2021
a) (P) có đỉnh I(-1; -2)
\(\Leftrightarrow\left\{{}\begin{matrix}-\dfrac{b}{2a}=-1\\-\dfrac{\Delta}{4a}=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=2a\\\dfrac{b^2-4ac}{4a}=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}b=2.2\\b^2-4.2.c=8.2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=4\\b^2-8c=16\end{matrix}\right.\Leftrightarrow4^2-8c=16\)
\(\Leftrightarrow c=0\)
=> y = 2x2 + 4x
b) (P) có trục đối xứng x = 1 và cắt trục tung tại M(0; 4)
\(M\in\left(P\right)\Rightarrow4=2.0^2+b.0+c\)
\(\Leftrightarrow c=4\)
Trục đối xứng: \(x=-\dfrac{b}{2a}=1\)
<=> -b = 2a
<=> -b = 2.2
<=> b = -4
=> y = 2x2 - 4x + 4
c) Đi qua 2 điểm A(1; 6), B(-1; 0)
\(A\in\left(P\right)\Rightarrow6=2.1^2+b.1+c\)
\(\Leftrightarrow b+c=4\) (1)
\(B\in\left(P\right)\Rightarrow0=2.\left(-1\right)^2+b\left(-1\right)+c\)
\(\Leftrightarrow-b+c=-2\) (2)
Từ (1) và (2) \(\Rightarrow\left\{{}\begin{matrix}b+c=4\\-b+c=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=3\\c=1\end{matrix}\right.\)
=> y = 2x2 + 3x + 1
NT
0
14 tháng 7 2019
Số ngày lớn nhất trong một tháng là 31,và các số nguyên tố nhỏ hơn 31 là 11;13;17.
Vậy 3 số áo là 11;13;17 và ba tổng đôi một của chúng là 24;28;30.
Vì các ngày nói đến trong câu truyện nằm trong cùng một tháng ,nên ngày sinh của Caitlin lớn nhất ,tức bằng 30,ngày hôm nay là 28,và ngày sinh của Bethany là 24.
Vậy số áo của Aslay là 13,của Bethany là 17 còn Caitline áo số 11.
Đáp án: A
28 tháng 5 2023
Đây là bài toán khá thú vị và không quá khó để giải. Vì tất cả các ngày nói đến trong câu chuyện nằm trong cùng một tháng, nên ngày sinh của Caitlin lớn nhất, tức là bằng 30, ngày hôm nay là 28 và ngày sinh của Bethany là 24. Từ đó dễ dàng tìm được số áo của Ashley là 13, của Bethany là 17 còn Caitlin mang áo số 11.
22 tháng 8 2019
Solution:
Dạng tổng quát :
\(\sqrt{1+k^2+\frac{k^2}{\left(k-1\right)^2}}=\sqrt{\frac{\left(1+k^2\right)\left(k+1\right)^2+k^2}{\left(k-1\right)^2}}\)
\(=\sqrt{\frac{k^4-2k^3+3k^2-2k+1}{\left(k-1\right)^2}}=\sqrt{\frac{\left(k^2-k\right)^2+2\left(k^2-k\right)+1}{\left(k-1\right)^2}}\)
\(=\sqrt{\frac{\left(k^2-k+1\right)^2}{\left(k-1\right)^2}}=\frac{k^2-k+1}{k-1}\)
\(=\frac{k\left(k-1\right)+1}{k-1}=k+\frac{1}{k-1}\)
Áp dụng ta có :
\(S=\sqrt{1+2020^2+\frac{2020^2}{2019^2}}-\frac{2020}{2019}\)
\(S=2020+\frac{1}{2019}-\frac{2020}{2019}\)
\(S=2020+\frac{-2019}{2019}\)
\(S=2020-1\)
\(S=2019\)
Vậy...
TT
2
N
18 tháng 3 2019
\(\Leftrightarrow mx^2-x+m-1< 0\)
\(\Rightarrow mx^2-x+m-1=0vong_0\)
\(\Rightarrow m< 0\)
18 tháng 3 2019
\(mx^2+m-1< x\)
\(\Leftrightarrow mx^2-x+m-1< 0\)
Để bpt vô nghiêm thì \(\left\{{}\begin{matrix}a>0\\\Delta< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\-4m^2+4m+1< 0\end{matrix}\right.\Leftrightarrow}\left\{{}\begin{matrix}m>0\\\left[{}\begin{matrix}m>\frac{1+\sqrt{2}}{2}\\m< \frac{1-\sqrt{2}}{2}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow}m>\frac{1+\sqrt{2}}{2}}\)
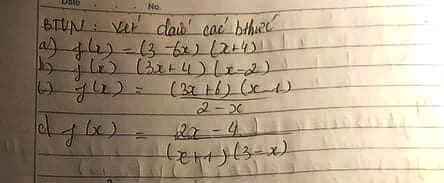
WTF TÍNH GÌ VẬY CẬU
cậu tính được hok nè