CK
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
10 tháng 7 2016
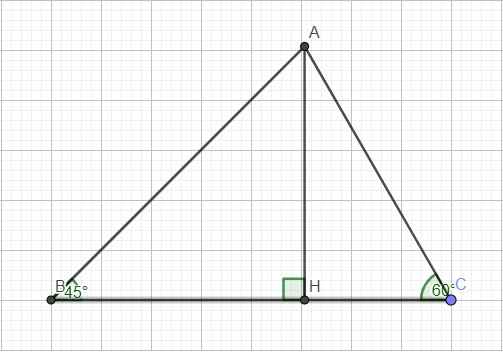
kẻ đường cao AH đặt AH=x
tam giác AHB có góc AHB=90 độ=>góc HAB=góc HBA=45 độ
=>tam giác AHB vuông cân tại H=>BH=AH=x
tam giác AHC vuông tại H=> \(AC^2=AH^2+HC^2=x^2+\left[2-x\right]^2\)[1]
tam giác AHC có góc H=90độ góc C=30 độ => góc HAC=60 độ=> \(HC=\frac{AC.\sqrt{3}}{2}suyraAC=\frac{2HC}{\sqrt{3}}suyraAC^2=\frac{4HC^2}{3}\)[2]
[1,2]=>\(x^2+\left[2-x\right]^2=\frac{4\left[2-x\right]^2}{3}\)
giải phương trình =>x=\(\sqrt{3}-1\)
Sabc=1/2.BC.AH=\(\frac{1}{2}.2.\left[\sqrt{3}-1\right]=\sqrt{3}-1cm^2\)
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 7 2021
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ABH ta có:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH ta có:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{\left(2a\right)^2}{2\left(cot45^0+cot60^0\right)}=\left(3-\sqrt{3}\right)a^2\)
25 tháng 9 2021
\(a,\sin A=\sin30^0=\dfrac{CP}{AC}=\dfrac{1}{2}\Rightarrow CP=4\left(cm\right)\)
\(b,\cos\widehat{PCB}=\cos50^0=\dfrac{CP}{BC}\approx0,64\Leftrightarrow BC=6,25\left(cm\right)\)
\(c,\cos A=\cos30^0=\dfrac{AP}{AC}=\dfrac{\sqrt{3}}{2}\Leftrightarrow AP=4\sqrt{3}\left(cm\right)\\ \sin\widehat{PCB}=\sin50^0=\dfrac{BP}{BC}\approx0,77\Leftrightarrow BP=4,8125\left(cm\right)\\ \Leftrightarrow AB=4,8125+4\sqrt{3}\\ \Leftrightarrow S_{ABC}=\dfrac{1}{2}CP\cdot AB=2\left(4,8125+4\sqrt{3}\right)\left(cm^2\right)\)
24 tháng 9 2021
a: Xét ΔACP vuông tại P có
\(CP=AC\cdot\sin30^0\)
\(=8\cdot\dfrac{1}{2}=4\left(cm\right)\)
24 tháng 9 2021
a: Xét ΔACP vuông tại P có
\(CP=AC\cdot\sin30^0\)
\(=8\cdot\dfrac{1}{2}=4\left(cm\right)\)