LK
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
tính nhanh p/s 1+ 5/4 + 5/8 + 5/16 + 5/32 + 5/64
9 tháng 5 2023
b: A=1/3+1/9+...+1/3^10
=>3A=1+1/3+...+1/3^9
=>A*2=1-1/3^10=(3^10-1)/3^10
=>A=(3^10-1)/(2*3^10)
c: C=3/2+3/8+3/32+3/128+3/512
=>4C=6+3/2+...+3/128
=>3C=6-3/512
=>C=1023/512
d: A=1/2+...+1/256
=>2A=1+1/2+...+1/128
=>A=1-1/256=255/256
CP
1
ND
2
HT
25 tháng 10 2020
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
đặt A = \(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(A\cdot2=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\)
\(A\cdot2-A=\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)\) \(-\) \(\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\right)\)
\(A=\) \(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}-\frac{1}{2}-\frac{1}{4}-\frac{1}{8}-\frac{1}{16}-\frac{1}{32}-\frac{1}{64}-\frac{1}{128}\)
\(A=1-\frac{1}{128}\)
\(A=\frac{127}{128}\)
ND
25 tháng 10 2020
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
Ta lấy\(\frac{1}{128}\)là MSC. Ta tính được \(\frac{64}{128}+\frac{32}{128}+\frac{16}{128}+\frac{8}{128}+\frac{4}{128}+\frac{2}{128}+\frac{1}{128}\)
Kết quả bằng \(\frac{127}{128}\)
HH
5
TH
14 tháng 1 2018
1/2 + 1/4 + 1/8 + 1/16 +1/32 + 1/64 + 1/128
=1-1/2+1/2-1/4+1/4-1/8+...+1/64+1/128
=1-1/128
=127/128
TD
18 tháng 3 2017
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+...+\frac{1}{64}-\frac{1}{128}\)
\(=1-\frac{1}{128}\)
\(=\frac{127}{128}\)
BT
18 tháng 3 2017
A=\(\frac{1}{2}\left(1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}\right)=\frac{1}{2}\left(1+A-\frac{1}{2}-\frac{1}{128}\right)\)
2A=\(A+\frac{1}{2}-\frac{1}{128}=A+\frac{63}{128}\)
=> A=\(\frac{63}{128}\)
TP
3
1 tháng 8 2016
A = 1/2 + 1/4 + 1/8 + ... + 1/1024
2A = 1 + 1/2 + 1/4 + ... + 1/512
2A - A = (1 + 1/2 + 1/4 + ... + 1/512) - (1/2 + 1/4 + 1/8 + ... + 1/1024)
A = 1 - 1/1024
A = 1023/1024
1 tháng 8 2016
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+....+\frac{1}{1024}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+......+\frac{1}{512}\)
\(\Rightarrow A=2A-A=1-\frac{1}{1024}\)
\(A=\frac{1023}{1024}\)
PN
0
U
5
19 tháng 3 2020
1/2 + 1/4+ 1/8+ 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512
= 1 – 1/2 + 1/2- 1/4 + 1/4 – 1/8 + 1/8 – 1/16 + 1/16 – 1/32 + 1/32 – 1/64 + 1/64 – 1/128 + 1/128 – 1/256 – 1/256 – 1/512
= 1 – 1/512
= 511/512 .
19 tháng 3 2020
Câu hỏi của Speed of light - Toán lớp 4 - Học toán với OnlineMath
Em tham khảo bài đc OLM k đúng nhé!
24 tháng 9 2017
voloc
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\)
\(A=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{4}+\frac{1}{4}-\frac{1}{6}+\frac{1}{6}-\frac{1}{8}+....+\frac{1}{64}-\frac{1}{128}\)
\(A=1-\frac{1}{128}\)
\(A=\frac{127}{128}\)
24 tháng 9 2017
\(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}.\)
\(=\frac{1}{1.2}+\frac{1}{2.2}+...+\frac{1}{64.2}\)
Rồi còn lại bạn tự giải nha
CHúc bạn học tốt
NB
2
B
12 tháng 5 2019
a ) \(\left(\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{64}+\frac{1}{128}\right)\times1280\)
= \(\frac{1}{2}\times1280+\frac{1}{4}\times1280+\frac{1}{8}\times1280+\frac{1}{16}\times1280+\frac{1}{32}\times1280+\frac{1}{64}\times1280\)\(+\frac{1}{128}\times1280\)
= 640 + 320 + 160 + 80 + 40 + 20 + 10
= ( 640 + 160 ) + ( 320 + 80 ) + ( 40 + 20 + 10 )
= 800 + 400 + 70
= 1270
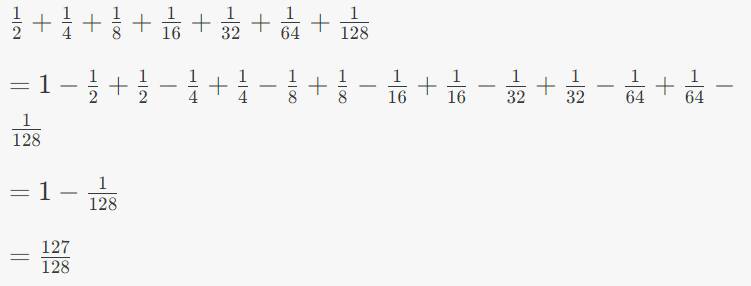
A = \(\dfrac{321}{963}\) + \(\dfrac{234}{468}\) - \(\dfrac{666}{1998}\)
A = \(\dfrac{1}{3}\) + \(\dfrac{1}{2}\) - \(\dfrac{1}{3}\)
A = 1/2
B = \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + \(\dfrac{1}{64}\) + \(\dfrac{1}{128}\)
2xB = 1 + \(\dfrac{1}{2}\) + \(\dfrac{1}{4}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{16}\) + \(\dfrac{1}{32}\) + \(\dfrac{1}{64}\)
2x B - B = 1 - \(\dfrac{1}{128}\)
B = \(\dfrac{127}{128}\)