Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Thu gọn M = - 5 a 2 từ đó tính được M = -125.
b) Gợi ý 15 = x + 1; 16 = x + 2; 29 = 2x + 1; 13 = x – 1.
Rút gọn N = -x, từ đó tính được N = -14.

b) Tại x=14 thì:\(B\left(x\right)=x^5-15x^4+16x^3-29x^2+13x\)
\(=x^5-\left(x+1\right)x^4+\left(x+2\right)x^3-\left(2x+1\right)x^2+x\left(x-1\right)\)
\(=x^5-x^5-x^4+x^4+2x^3-2x^3-x^2+x^2-x=-x=-14\)
a) A(x)=1

b) Ta có: \(B=5x\left(x-4y\right)-4y\left(y-5x\right)\)
\(=5x^2-20xy-4y^2+20xy\)
\(=5x^2-4y^2\)
\(=5\cdot\left(-\dfrac{1}{5}\right)^2-4\cdot\left(-\dfrac{1}{2}\right)^2\)
\(=5\cdot\dfrac{1}{25}-4\cdot\dfrac{1}{4}\)
\(=\dfrac{1}{5}-1=\dfrac{-4}{5}\)

a: Ta có: x=31
nên x-1=30
Ta có: \(A=x^3-30x^2-31x+1\)
\(=x^3-x^2\left(x-1\right)-x^2+1\)
\(=x^3-x^3+x^2-x^2+1\)
=1
c: Ta có: x=16
nên x+1=17
Ta có: \(C=x^4-17x^3+17x^2-17x+20\)
\(=x^4-x^3\left(x+1\right)+x^2\left(x+1\right)-x\left(x+1\right)+20\)
\(=x^4-x^4-x^3+x^3+x^2-x^2-x+20\)
\(=20-x=4\)
d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=10-x\)
=-2

d: Ta có: x=12
nên x+1=13
Ta có: \(D=x^{10}-13x^9+13x^8-13x^7+...+13x^2-13x+10\)
\(=x^{10}-x^9\left(x+1\right)+x^8\left(x+1\right)-x^7\left(x+1\right)+...+x^2\left(x+1\right)-x\left(x+1\right)+10\)
\(=x^{10}-x^{10}-x^9+x^9+x^8-x^8-x^7+...+x^3+x^2-x^2-x+1+9\)
\(=-x+10=-2\)
các bạn giải hộ mình với :
a,X3 - 30X2 - 31X + 1 với X = 31
b,X5 - 15X4 + 16X3 - 29X2 + 13X với X = 14


\(M=x^5-15x^4+16x^3-29x^2+13x\)
\(=x^5-14x^4-x^4+14x^3+2x^3-28x^2-x^2+14x-x\)
\(=x^4\left(x-14\right)-x^3\left(x-14\right)+2x^2\left(x-14\right)-x\left(x-14\right)-x\)
\(=\left(x^4-x^3+2x^3-x\right)\left(x-14\right)-x\)
Thay \(x=14\) vào biểu thức M, ta có:
\(M=\left(14^4-14^3+2.14^2-14\right)\left(14-14\right)-14\)
\(=0-14\)
\(=-14\)

\(B=x^5-15x^4+16x^3-29x^2+13x\)
\(=x^5-14x^4-x^4+14x^3+2x^3-28x^2-x^2+14x-x+14-14\)
\(=x^4\left(x-14\right)-x^3\left(x-14\right)+2x^2\left(x-14\right)-x\left(x-14\right)-\left(x-14\right)-14\)
\(=\left(x^4-x^3+2x^2-x-1\right)\left(x-14\right)-14\)
Thay x = 14 => B = -14
Vậy...
phần còn lại tách ra làm tương tự nhé
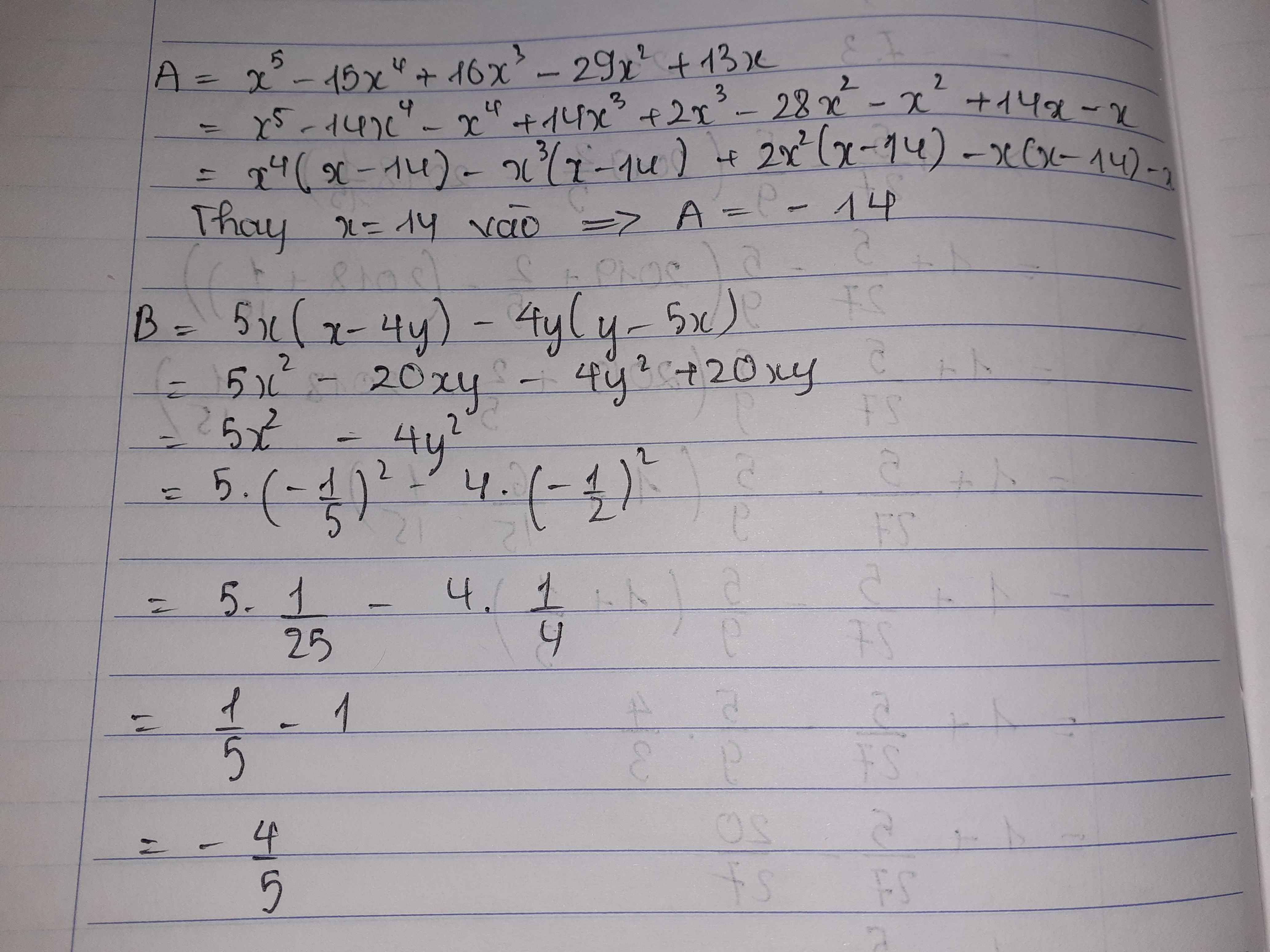
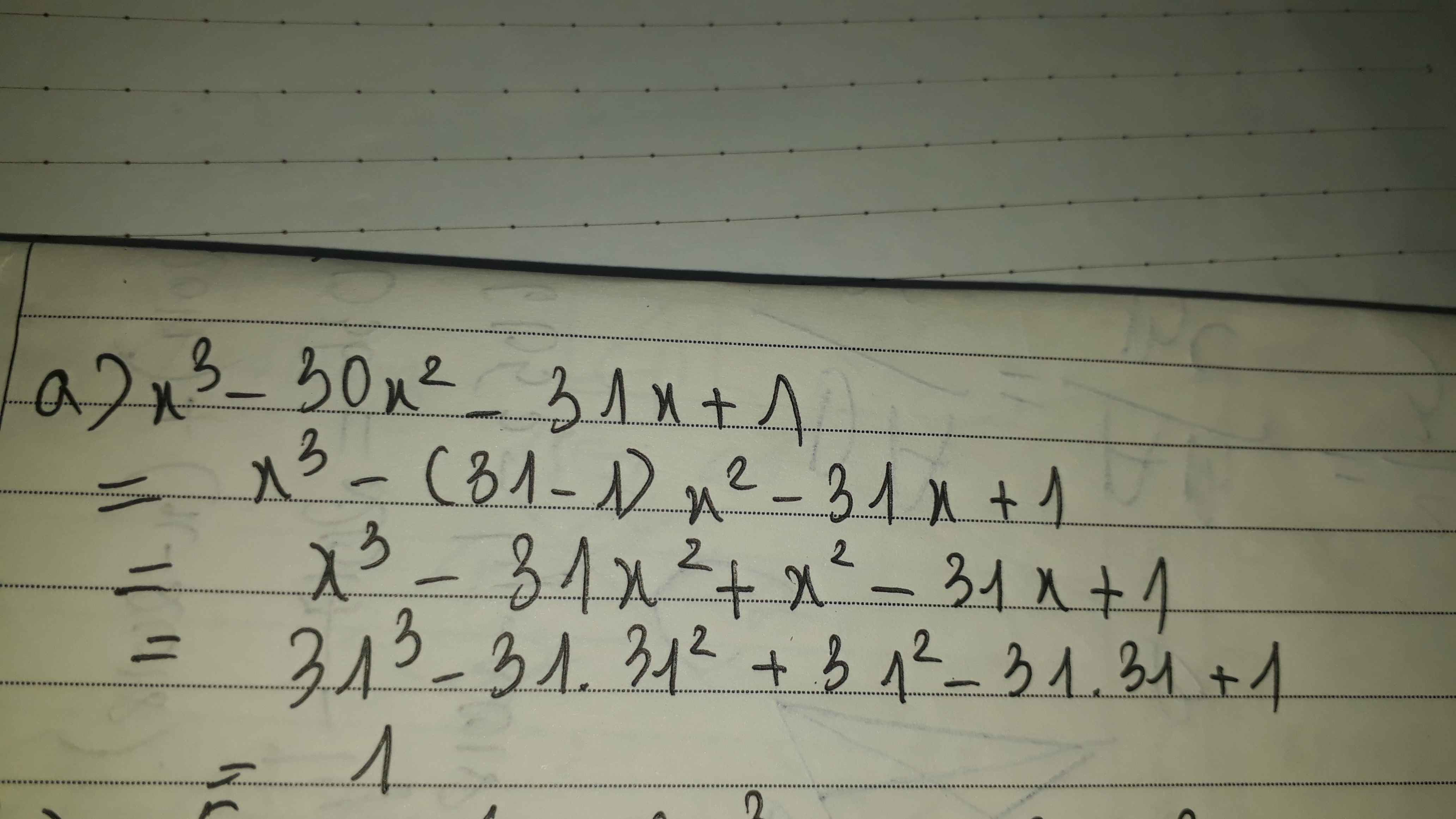


\(C=x^5-15x^4+16x^3-29x^2+13x\)
\(C=x^5-14x^4-x^4+14x^3+2x^3-28x^2-x^2+14x-x\)
\(C=x^4\left(x-14\right)-x^3\left(x-14\right)+2x^2\left(x-14\right)-x\left(x-14\right)-x\)
\(C=\left(x^4-x^3+2x^2-x\right)\left(x-14\right)-x\)
Thay \(x=14\) vào \(C\):
\(\Rightarrow C=\left(14^4-14^3+2.14^2-14\right)\left(14-14\right)-14\)
\(C=0-14=-14\)
Vậy \(C=-14\) tại \(x=14\)