K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
19 tháng 8 2018
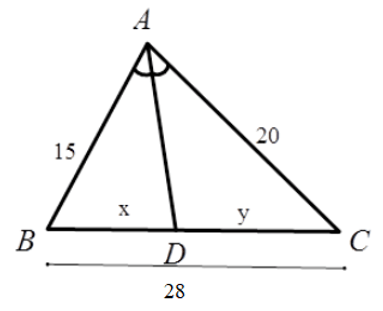
Vì AD là phân giác góc B A C ^ nên ta có: B D D C = A B A C = 15 20 = 3 4
⇒ B D D C = 3 4 ⇒ B D B D + D C = 3 4 + 3 = 3 7 ⇔ B D B C = 3 7 ⇒ x 28 = 3 7
=> x = 12cm => y = 28 – x = 16 cm
Vậy x = 12cm; y = 16cm
Đáp án: D
PT
1
CM
1 tháng 5 2018
Trong tam giác ABC, ta có: MN // BC
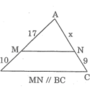
Suy ra: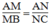 
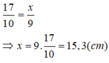
Trong tam giác PQR, ta có: EF // QR
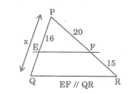
Suy ra: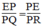 
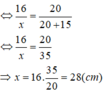
16 tháng 9 2021
Giả sử hình thang ABCD, đường trung bình MN \(\left(M\in AD;N\in BC\right)\) và AC cắt MN tại P
Ta có \(\left\{{}\begin{matrix}MP+PN=10\\MP-PN=2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}MP=\left(10+2\right):2=6\left(cm\right)\\PN=10-6=4\left(cm\right)\end{matrix}\right.\)
Vì MN là đtb nên: \(MN//AB//CD;MN=\dfrac{AB+CD}{2}.hay.AB+CD=2MN=20\)
\(\left\{{}\begin{matrix}AM=MD\\MP//CD\end{matrix}\right.\Rightarrow AP=PC\Rightarrow PM\) là đtb \(\Delta ADC\)
\(\Rightarrow2PM=DC\Rightarrow DC=2\cdot6=8\left(cm\right)\\ \Rightarrow AB=20-8=12\left(cm\right)\)
Vậy 2 đáy hình thang là 8;12(cm)
SG
1
22 tháng 4 2017
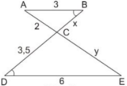
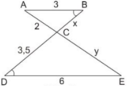
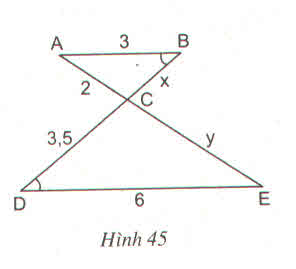
ABDABD^ = ˆBDEBDE^, lại so le trong
=> AB // DE
=> ∆ABC ∽ ∆EDC
=> ABEDABED = BCDCBCDC = ACECACEC
=> 3636 = x3,5x3,5 = 2y2y
=> x = 3.3,563.3,56 = 1.75;
y = 6.236.23 = 4
15 tháng 3 2023
vì góc ADB = góc BDE
=>AB // DE (so le trong)
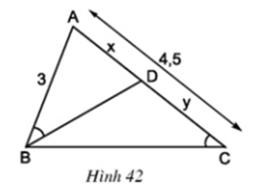
vì AB//DE nên theo định lí ta - lét ta có :
\(\dfrac{CB}{CE}\) = \(\dfrac{CA}{CD}\)
=>\(\dfrac{x}{y}\) = \(\dfrac{2}{3,5}\) = \(\dfrac{4}{7}\)
vậy chiều dài CB là 4
CE là 7
L
13 tháng 2 2022
Theo tính chất tpg của tam giác, ta có:
\(\dfrac{AB}{BD}=\dfrac{AC}{DC}\)
Áp dụng dãy tỉ số bằng nhau, ta có:
\(\dfrac{AB}{x}=\dfrac{AC}{y}=\dfrac{15+20}{x+y}=\dfrac{35}{28}\) = 1,25
\(\Rightarrow x=\dfrac{15}{1,25}=12cm\)
\(\Rightarrow y=\dfrac{20}{1,25}=16cm\)
\(\RightarrowĐáp.án.D\)
CM
19 tháng 9 2018
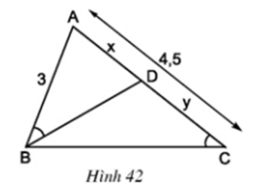
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
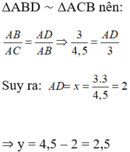
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
CM
19 tháng 12 2018
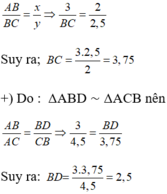
a) Trong hình vẽ có 3 tam giác: ΔABD, ΔCBD, ΔABC
ΔABD và ΔACB có
∠B = ∠C
∠A chung
⇒ ΔABD ∼ ΔACB (g.g)
b) Theo a ta có :
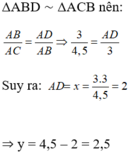
c) Do BD là tia phân giác của góc B nên theo tính chất đường phân giác ta có:
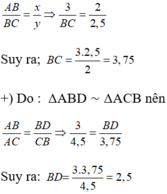
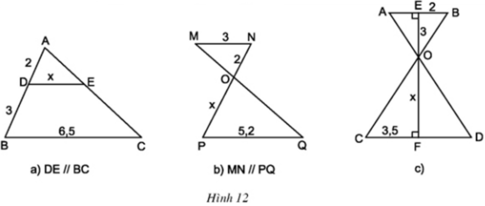
Áp dụng hệ quả định lí Ta – lét ta có:
- Hình a:
- Hình b:
- Hình c: