
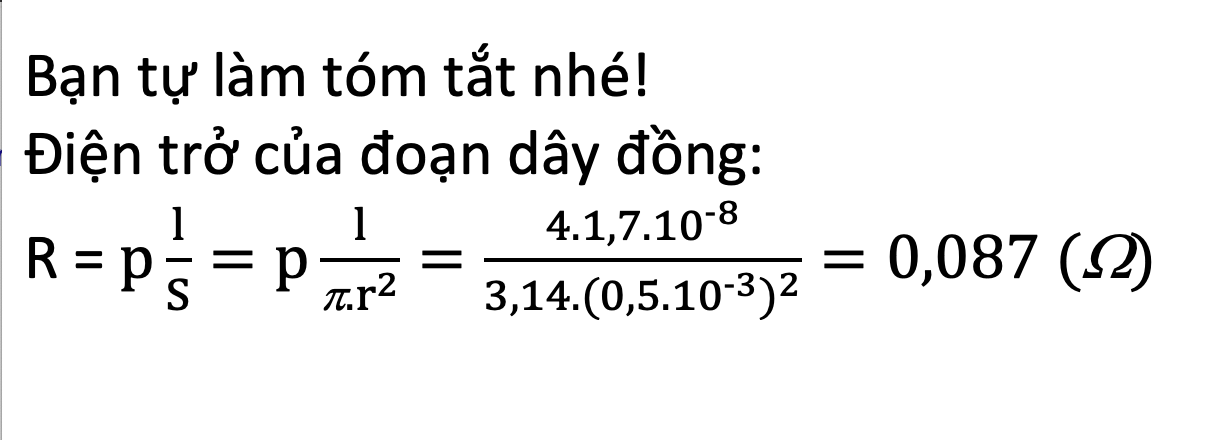
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

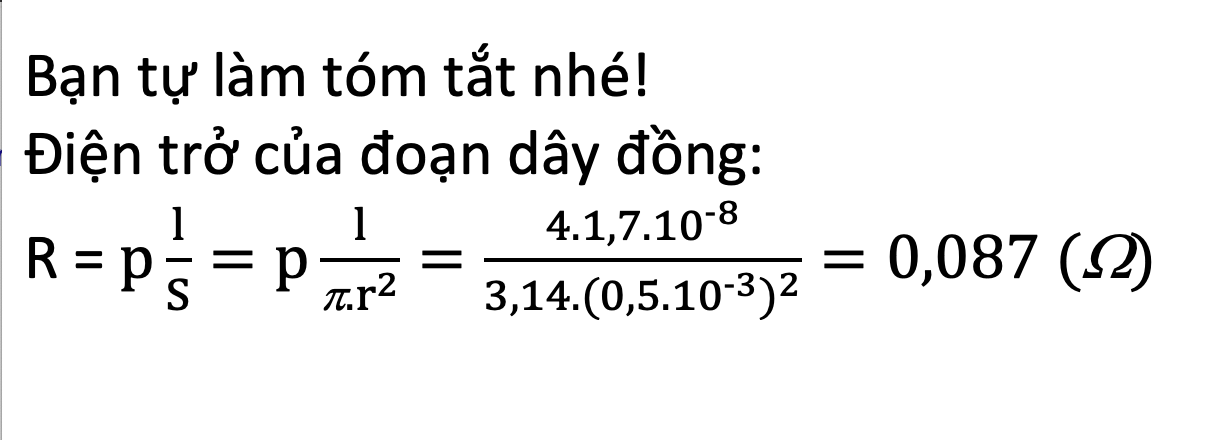

ta có \(R=\dfrac{pl}{s}\)=\(1,7\cdot10^{-8}\cdot\dfrac{4}{3,14\cdot\left(0,5\cdot10^{-3}\right)^2}\)
=0.087\(\Omega\)
C4. Tính điện trở của đoạn dây đồng dài l = 4 m có tiết diện tròn, đường kính d = 1 mm (lấy π = 3,14).
Hướng dẫn.
Ta có R = = 1,7.10-8.=
= 0,087 Ω.

\(\Rightarrow\left\{{}\begin{matrix}R=\dfrac{pl}{S}\Rightarrow S=\dfrac{pl}{R}=\dfrac{1,7.10^{-8}.4}{0,087}=7,816.10^{-7}m^2\\S=\left(\dfrac{d}{2}\right)^2\pi\Rightarrow d=\sqrt{\dfrac{4S}{\pi}}=\sqrt{\dfrac{4.7,816.10^{-7}}{\pi}}=9,98.10^{-4}m\end{matrix}\right.\)

Tiết diện dây dẫn:
\(S=\pi R^2=\pi\cdot\left(\dfrac{d}{2}\right)^2=\pi\cdot\left(\dfrac{0,6\cdot10^{-3}}{2}\right)^2=2,83\cdot10^{-7}m^2\)
Điện trở dây:
\(R=\rho\cdot\dfrac{l}{S}=0,4\cdot10^{-6}\cdot\dfrac{9}{S}\approx12,73\Omega\)

Điện trở dây:
\(R=\rho\cdot\dfrac{l}{S}=1,7\cdot10^{-8}\cdot\dfrac{10}{\pi\cdot\dfrac{d^2}{4}}=1,7\cdot10^{-8}\cdot\dfrac{10}{\pi\cdot\dfrac{\left(0,1\cdot10^{-3}\right)^2}{4}}\approx21,64\Omega\)

TT
\(l=1m\)
\(R=8\Omega\)
\(\rho=0,4.10^{-6}\Omega m\)
\(\tau\tau=3,14\)
\(d=?m\)
Giải
Tiết diện của dây là:
\(R=\dfrac{\rho.l}{S}\Rightarrow S=\dfrac{\rho.l}{R}=\dfrac{0,4.10^{-6}.1}{8}=5,10^{-8}m^2\)
Đường kính tiết diện của dây là:
\(S=\dfrac{\tau\tau.d^2}{4}\Rightarrow d=\sqrt{\dfrac{S.4}{\tau\tau}}=\sqrt{\dfrac{5.10^{-8}.4}{3,14}}\approx1,7.10^{-3}m\)

a) \(R=\rho\cdot\dfrac{l}{S}=1,7\cdot10^{-8}\cdot\dfrac{l}{3\cdot10^{-6}}=9,4\)
\(\Rightarrow l=1658,82m\)
b) \(R=\rho\cdot\dfrac{l}{S}=2,82\cdot10^{-8}\cdot\dfrac{1,2}{1\cdot10^{-6}}=0,03384\Omega\)