
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có:
\(A=3+\frac{3}{1+2}+\frac{3}{1+2+3}+...+\frac{3}{1+2+3+4+...+100}\)
\(A=3\left(1+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+4+...+100}\right)\)
Đặt \(B=1+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+4+...+100}\), khi đó ta đc:
\(B=1+\frac{1}{1+2}+\frac{1}{1+2+3}+...+\frac{1}{1+2+3+4+...+100}\)
Vì tổng số hạng bằng (số cuối + số đầu) . số số hạng : 2 nên ta có:
\(B=1+\frac{1}{\left(1+2\right).2:2}+\frac{1}{\left(1+3\right).3:2}+\frac{1}{\left(1+4\right).4:2}+...+\frac{1}{\left(1+100\right).100:2}\)
\(B=\frac{2}{1.2}+\frac{2}{2.3}+\frac{2}{3.4}+\frac{2}{4.5}+...+\frac{2}{100.101}\)
\(B=2\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{100.101}\right)\)
\(B=2\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{100}-\frac{1}{101}\right)\)
\(B=2.\left(1-\frac{1}{101}\right)\)
\(B=2.\frac{100}{101}=\frac{200}{101}\)
Ta có:
\(A=3.B\Rightarrow A=3.\frac{200}{101}=\frac{600}{101}\)
Vậy \(A=\frac{600}{101}\)

\(1^2-2^2+3^2-4^2+5^2-6^2+........+99^2-100^2\)
\(=\left(1^2-2^2\right)+\left(3^2-4^2\right)+\left(5^2-6^2\right)+........+\left(99^2-100^2\right)\)
\(=\left(1+2\right)\left(1-2\right)+\left(3+4\right)\left(3-4\right)+\left(5+6\right)\left(5-6\right)........+\left(99+100\right)\left(99-100\right)\)
\(=-1\left(1+2\right)+-1\left(3+4\right)+-1\left(5+6\right)+........+-1\left(99+100\right)\)
\(=-1\left[\left(1+2\right)+\left(3+4\right)+\left(5+6\right)+........+\left(99+100\right)\right]\)
\(=-1\left(3+7+11+........+199\right)\)
\(=-1.\left\{\dfrac{\left(199+3\right).\left[\left(199-3\right):4+1\right]}{2}\right\}\)
\(=-1.\left[\dfrac{202.\left(196:4+1\right)}{2}\right]\)
\(=-1.\left[\dfrac{202.\left(49+1\right)}{2}\right]\)
\(=-1.\dfrac{202.50}{2}\)
\(=-1.\dfrac{10100}{2}\)
\(=-1.5050\)
\(=-5050\)

a) Áp dụng công thức là xong hết có gì khó đâu
Ta có số số hạng của dãy số: \(\dfrac{\left(100-1\right)}{1}+1=99+1=100\)
Tổng của dãy số: \(\left(100+1\right).100:2\) = 5050
b) Ta có: \(\dfrac{5}{4}-\dfrac{1}{100}.25=\dfrac{5}{4}-\dfrac{25}{100}=\dfrac{5}{4}-\dfrac{1}{4}=\dfrac{4}{4}=1\)

Bài 1:
a) \(S=1+2+3+4+5+6+7+8+9\)
\(=\left(1+9\right)+\left(2+8\right)+\left(3+7\right)+\left(4+6\right)+5\)
\(=10+10+10+10+5\)
\(=45\)
b) lm như bài này: Câu hỏi của Thái Minh Tuệ - Toán lớp 4 - Học toán với OnlineMath
S=(1+9)+(2+8)+(3+7)+(4+6)+5=10+10+10+10+5![]()
M=so so hang cua tong M la
(101-1):1+1=101
tong cua M la
(101+1):2x101=5151


Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
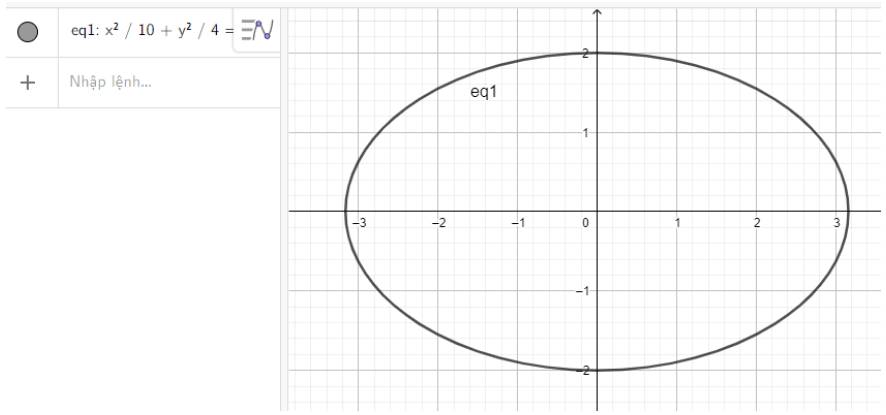
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
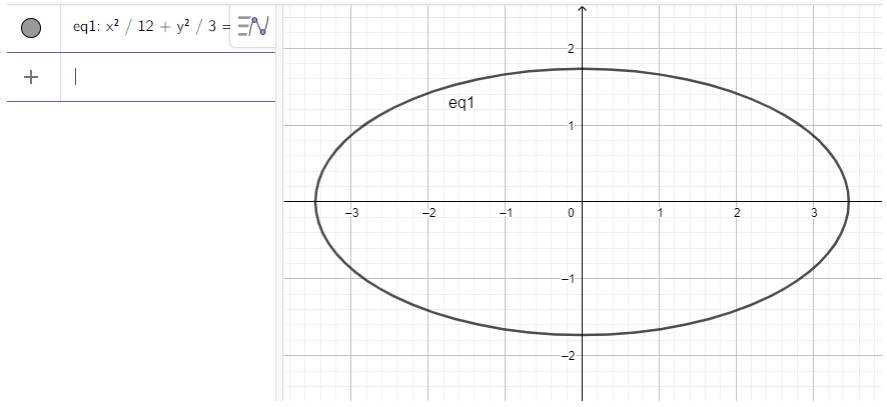
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
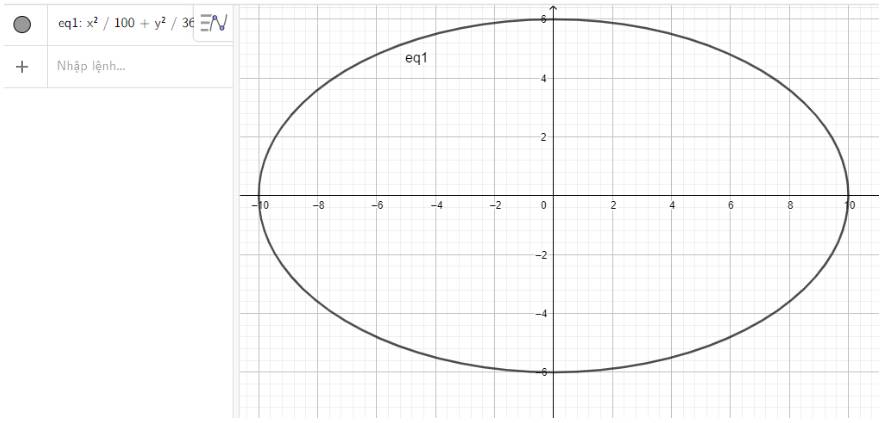

a: \(=\dfrac{54-34}{189-119}=\dfrac{20}{70}=\dfrac{2}{7}\)
b: \(=\dfrac{6+6\cdot4+6\cdot49}{15+15\cdot4+15\cdot49}=\dfrac{6}{15}=\dfrac{2}{5}\)
c: \(=\dfrac{13\left(3-18\right)}{40\left(15-2\right)}=\dfrac{-15}{40}=-\dfrac{3}{8}\)