Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: \(=\dfrac{1}{29\cdot30}-\left(\dfrac{1}{1\cdot2}+\dfrac{1}{2\cdot3}+...+\dfrac{1}{28\cdot29}\right)\)
\(=\dfrac{1}{29\cdot30}-\left(1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{28}-\dfrac{1}{29}\right)\)
\(=\dfrac{1}{29\cdot30}-\dfrac{28}{29}=\dfrac{1-28\cdot30}{870}=\dfrac{-859}{870}\)

Dựa vào bảng tần số, ta thấy tần số lớn nhất là 47 ứng với cỡ áo 39. Vậy mốt của mẫu số liệu là 39.

a) Ta cần tính cạnh BC và hai góc \(\widehat B,\widehat C.\)
Áp dụng định lí cosin, ta có:
\(\begin{array}{l}B{C^2} = A{B^2} + A{C^2} - 2.AB.AC.\cos A\\ \Leftrightarrow B{C^2} = {14^2} + {23^2} - 2.14.23.\cos {125^o}\\ \Rightarrow BC \approx 33\end{array}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{33}}{{\sin {{125}^o}}} = \frac{{23}}{{\sin B}} = \frac{{14}}{{\sin C}}\\ \Rightarrow \sin B = \frac{{23.\sin {{125}^o}}}{{33}} \approx 0,57\\ \Rightarrow \widehat B \approx {35^o} \Rightarrow \widehat C \approx {20^o}\end{array}\)
b) Ta cần tính góc A và hai cạnh AB, AC.
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {64^o} - {38^o} = {78^o}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{22}}{{\sin {{78}^o}}} = \frac{{AC}}{{\sin {{64}^o}}} = \frac{{AB}}{{\sin {{38}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}AC = \sin {64^o}.\frac{{22}}{{\sin {{78}^o}}} \approx 20,22\\AB = \sin {38^o}.\frac{{22}}{{\sin {{78}^o}}} \approx 13,85\end{array} \right.\end{array}\)
c) Ta cần tính góc A và hai cạnh AB, BC.
Ta có: \(\widehat A = {180^o} - \widehat B - \widehat C = {180^o} - {120^o} - {28^o} = {32^o}\)
Áp dụng định lí sin, ta có:
\(\begin{array}{l}\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} = \frac{{AB}}{{\sin C}} \Leftrightarrow \frac{{BC}}{{\sin {{32}^o}}} = \frac{{22}}{{\sin {{120}^o}}} = \frac{{AB}}{{\sin {{28}^o}}}\\ \Rightarrow \left\{ \begin{array}{l}BC = \sin {32^o}.\frac{{22}}{{\sin {{120}^o}}} \approx 13,5\\AB = \sin {28^o}.\frac{{22}}{{\sin {{120}^o}}} \approx 12\end{array} \right.\end{array}\)
d) Ta cần tính số đo ba góc \(\widehat A,\widehat B,\widehat C\)
Áp dụng hệ quả của định lí cosin, ta có:
\(\begin{array}{l}\cos A = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2.AB.AC}};\cos B = \frac{{B{C^2} + A{B^2} - A{C^2}}}{{2.BC.BA}}\\ \Rightarrow \cos A = \frac{{{{32}^2} + {{23}^2} - {{44}^2}}}{{2.32.23}} = \frac{{ - 383}}{{1472}};\cos B = \frac{{{{44}^2} + {{23}^2} - {{32}^2}}}{{2.44.23}} = \frac{{131}}{{184}}\\ \Rightarrow \widehat A \approx {105^o},\widehat B = {44^o}36'\\ \Rightarrow \widehat C = {30^o}24'\end{array}\)

Cách 1:
+ Giá trị đại diện mỗi lớp: c 1 = 18 ; c 2 = 22 ; c 3 = 26 ; c 4 = 30 ; c 5 = 34
+ Số trung bình cộng:
x = n 1 c 1 + n 2 c 2 + n 3 c 3 + n 4 c 4 + n 5 c 5 n 1 + n 2 + n 3 + n 4 + n 5 = 10 . 18 + 12 . 22 + 14 . 26 + 9 . 30 + 5 . 34 50 ≈ 25
+ Độ lệch chuẩn:
s = s 2 = 10 18 - 25 2 + 12 22 - 25 2 + 14 26 - 25 2 + 9 30 - 25 2 + 5 34 - 25 2 50
≈ 5 , 0
Cách 2: Sử dụng máy tính Casio fx - 570 VNPLUS
+ Nhập ![]() (vào chế thống kê).
(vào chế thống kê).
+ Nhập ![]() (hiển thị cột tần số).
(hiển thị cột tần số).
+ Nhập ![]() (nhập giá trị).
(nhập giá trị).
+ Nhập ![]() (nhập tần số), sau đó ấn
(nhập tần số), sau đó ấn ![]() .
.
+ Nhập ![]()
⇒ δ x = 4 , 983813801
(Lưu ý: Đối với Ví dụ 2, phương sai s 2 = 24 , 9 ).
Đáp án C.

1/ 32.( -39) + 16.( –22)
\(=2.16.\left(-39\right)+16.\left(-22\right)\)
\(=16.\left[2.\left(-39\right)+\left(-22\right)\right]\)
\(=16.\left[\left(-78\right)+\left(-22\right)\right]\)
\(=16.\left(-100\right)\)
\(=-1600\)
2/ 44.( –36) + 22.( –28)
\(=2.22.\left(-36\right)+22.\left(-28\right)\)
\(=22\left[2.\left(-36\right)+\left(-28\right)\right]\)
\(=22.\left[\left(-72\right)+\left(-28\right)\right]\)
\(=22.\left(-100\right)\)
\(=-2200\)

Gọi x là số xe chở được 45 khách, y là số xe chở được 12 khách. Ta có hệ phương trình
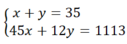
Nếu dùng máy tính cầm tay, ta nhập hệ phương trình vào máy, sẽ cho ngay kết quả là phương án C.
Nếu không dùng máy tính, ta có thể xét các phương án, với nhận xét là số xe 45 chỗ càng nhiều thì tổng số khách trở được càng lớn. Bắt đầu từ phương án A vì có số xe 45 chỗ là 20 dễ tính nhẩm, ta được tổng số khách chở được là 1080, ít hơn số 1113, nên phương án A bị loại. Các phương án B và D có số xe 45 chỗ ít hơn 20 nên số khách chở được càng ít hơn, nên B và D cũng bị loại.
Đáp án: C

\(\hept{\begin{cases}5x+5y=30\\y+5z=12\\3x+5z=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=6-y\\y+5z=12\\3x+5z=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+5z=12\\3\left(6-y\right)+5z=22\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+5z=12\\-3y+5z=4\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}y+5z=12\\3y-5z=-4\end{cases}}\)
\(\Rightarrow4y=8\Rightarrow y=2\)
Thay giá trị của y vào phương trình: -3y + 5z = 4
\(-3\times2+5z=4\)
\(\Rightarrow z=2\)
Thế giá trị của y vào phương trình: x = 6 - y
\(\Rightarrow x=4\)

Đường tròn (C) có phương trình: ( x - 2 ) 2 + ( y + 1 ) 2 = 4 có tâm I( 2; -1) và bán kính R = 2.
ĐÁP ÁN C

Gọi A là tập hợp các học sinh của lớp 10A;
V là tập hợp các học sinh giỏi môn Văn và T là tập hợp các học sinh giỏi môn Toán của lớp 10A.
Kí hiệu |X| là số phần tử của tập hợp hữu hạn X.
Ta có

Đáp án D
