
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ta có \(\left(x+2\right)^2-2\left(x+2\right)\left(x+3\right)+\left(x+5\right)^2=7\)
\(\Leftrightarrow x^2+4x+4-2\left(x^2+5x+6\right)+x^2+10x+25=7\)
\(\Leftrightarrow4x+10=0\Leftrightarrow x=-\frac{5}{2}\)
Bạn áp dụng hằng đẳng thức số 1, nhân phá ngoặc là Ok nhé
\(\left(x+2\right)^2-2\left(x+2\right)\left(x+3\right)+\left(x+5\right)^2=7\)
\(\Leftrightarrow x^2+4x+4-2\left(x^2+3x+2x+6\right)+x^2+10x+25-7=0\)
\(\Leftrightarrow2x^2+14x+22-2x^2-6x-4x-12=0\)
\(\Leftrightarrow4x+10=0\)
\(\Leftrightarrow4x=-10\)
\(\Leftrightarrow x=\frac{-5}{2}\)

Thôi làm thế này đi:3
\(A=-\frac{2xy}{1+xy}=-\frac{2\left(1+xy\right)+2}{1+xy}=\frac{2}{1+xy}-2\)
Áp dụng BĐT Cosi ta có:
\(xy\le\frac{x^2+y^2}{2}=\frac{1}{2}\)
\(\Rightarrow A\ge\frac{2}{1+\frac{1}{2}}-2=-\frac{2}{3}\)
Dấu "=" xảy ra khi \(\Leftrightarrow x=y=\frac{\sqrt{2}}{2}\)
vậy GTNNA = \(-\frac{2}{3}\Leftrightarrow x=y=\frac{\sqrt{2}}{2}\)
\(A=-\frac{2xy}{1+xy}=-2xy-2\)
Áp dụng BĐT Cosi ta có:
\(2xy\le x^2+y^2=1\)dấu "=" xảy ra khi:
\(\Leftrightarrow\hept{\begin{cases}x^2=y^2\\x^2+y^2=1\end{cases}}\Leftrightarrow x=y=\frac{\sqrt{2}}{2}\) (thỏa mãn ĐKXĐ vs x,y > 0 )
\(\Rightarrow A\ge-1-2=-3\)
dấu "=" xảy ra khi:
\(\Leftrightarrow x=y=\frac{\sqrt{2}}{2}\)(thỏa mãn ĐKXĐ vs x,y > 0 )
vậy GTNN \(A=-3\Leftrightarrow x=y=\frac{\sqrt{2}}{2}\)

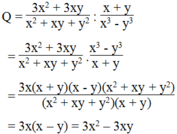
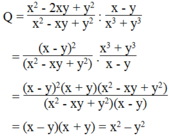
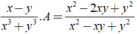
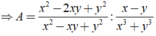
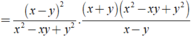
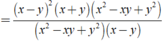
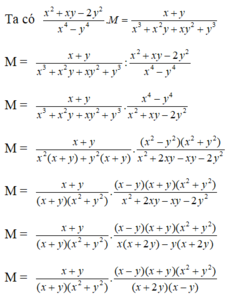
Ta có : x^3 + y^3 = 152
(x+y)(x^2-xy+y^2)=152 (1)
Thay x^2-xy+y^2=19 vào (1) ta được:
(x+y).19=152
->x+y=8
Mà x-y=2 nên => x=5 và y=3
Vậy x=5:y=3
bn có ghi thiếu để k?