

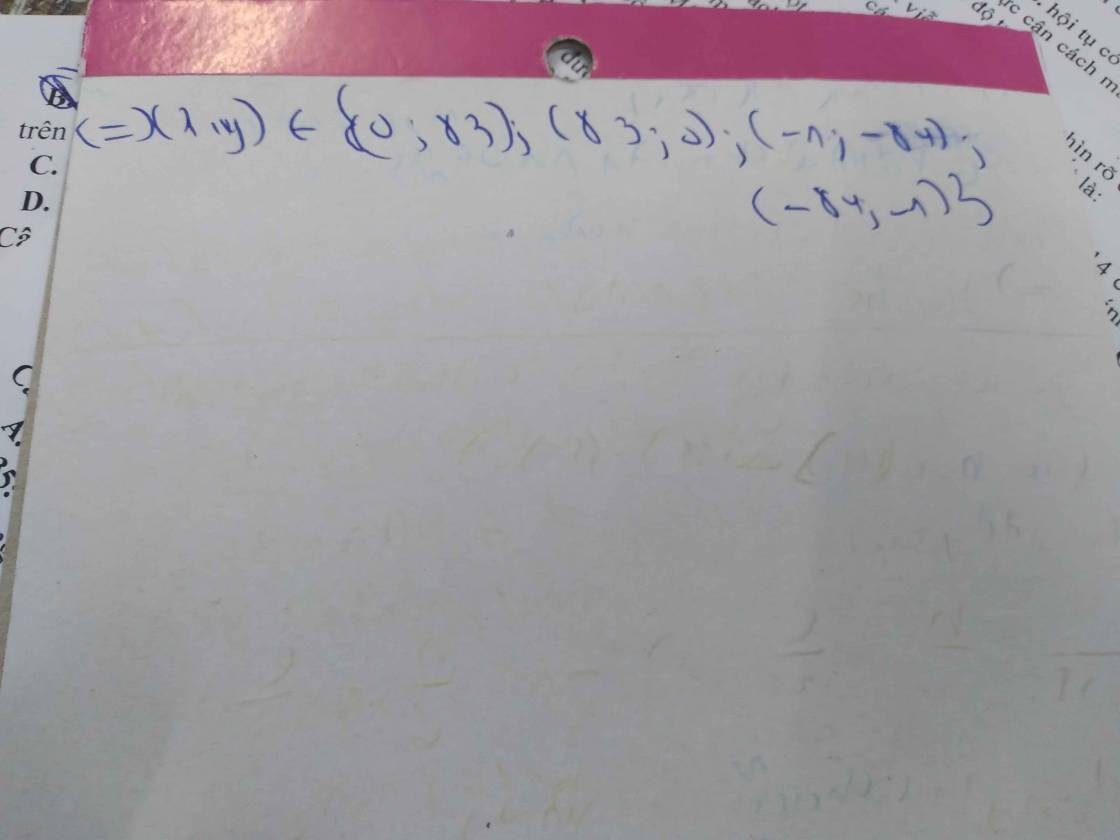
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


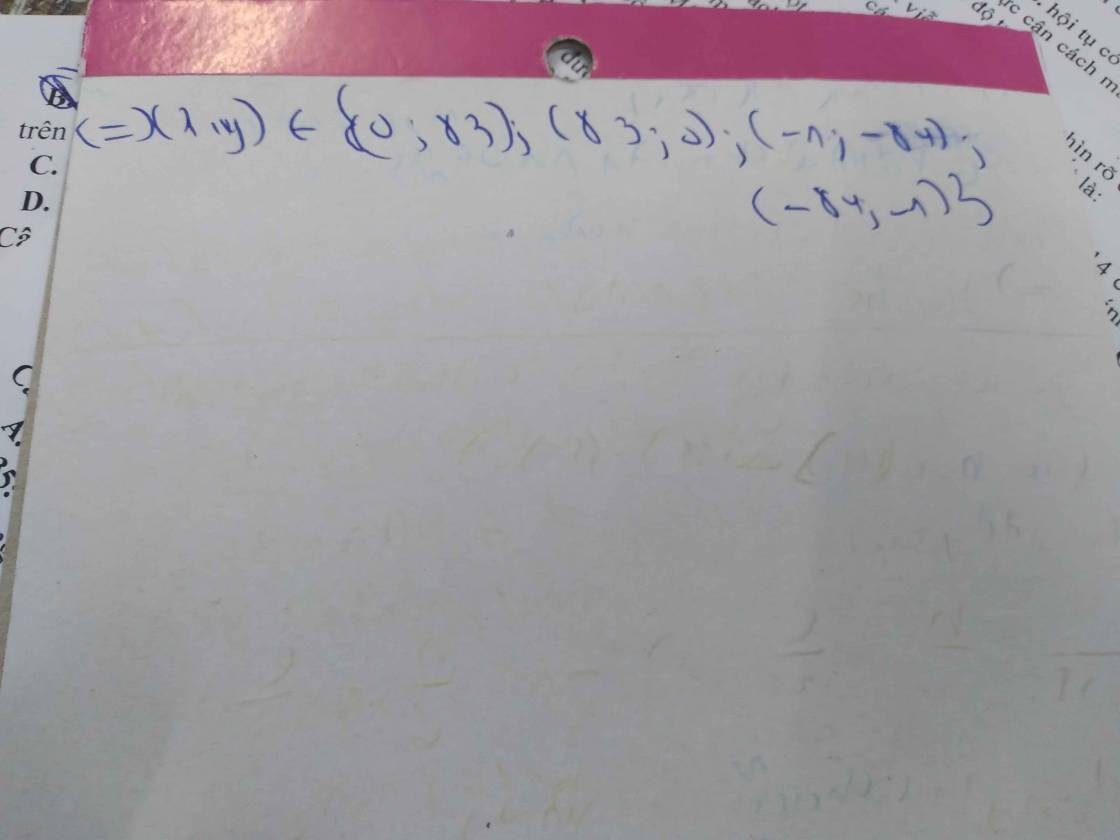



Ta có: 2xy+x+y=83\(\Rightarrow\)4xy+2x+2y=166\(\Rightarrow\)(2x+1) (2y+1)=167\(\Rightarrow\)x,y \(\in\)(0;83), (83;0)
Vì x,y nguyên dương nên ko tồn tại x,y
ta có:\(x+2xy+y=83\)
\(\Leftrightarrow x\left(1+2y\right)+\frac{1}{2}\left(1+2y\right)=\frac{167}{2}\)
\(\Leftrightarrow\left(x+\frac{1}{2}\right)\left(1+2y\right)=\frac{167}{2}\)
\(\Leftrightarrow\left(2x+1\right)\left(2y+1\right)=167=1.167=167.1\) (vì x,y>0)
với: \(\hept{\begin{cases}2x+1=1\\2y+1=167\end{cases}\Rightarrow\hept{\begin{cases}x=0\\y=83\end{cases}}}\)
với \(\hept{\begin{cases}2x+1=167\\2y+1=1\end{cases}\Rightarrow\hept{\begin{cases}x=83\\y=0\end{cases}}}\)
Vậy (x;y)={ (0;83) ; (83;0)}


\(\Leftrightarrow\left(x^2+y^2+1-2xy+2x-2y\right)+\left(y^2-4y+4\right)=4\)
\(\Leftrightarrow\left(x-y+1\right)^2+\left(y-2\right)^2=4=2^2+0^2=0^2+2^2\)
\(\Rightarrow x;y\)


a) Ta có: \(\left\{{}\begin{matrix}x+my=2\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+m^2y=2m\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m^2y+2y=2m-1\\mx-2y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y\left(m^2+2\right)=2m-1\\mx=1+2y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{2m-1}{m^2+2}\\x=\dfrac{1+2y}{m}=\left(1+\dfrac{2m-1}{m^2+2}\right)\cdot\dfrac{1}{m}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{m^2+2+2m-1}{m^2+2}\cdot\dfrac{1}{m}=\dfrac{m^2+2m+1}{m\left(m^2+2\right)}\\y=\dfrac{2m-1}{m^2+2}\end{matrix}\right.\)
Để hệ phương trình có nghiệm duy nhất thỏa mãn x>0 và y>0 thì \(\left\{{}\begin{matrix}\dfrac{m^2+2m+1}{m\left(m^2+2\right)}>0\\\dfrac{2m-1}{m^2+2}>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\2m-1>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m>0\\m>\dfrac{1}{2}\end{matrix}\right.\)
\(\Leftrightarrow m>\dfrac{1}{2}>0\)
Vậy: Khi m>0 thì hệ phương trình có nghiệm duy nhất (x,y) thỏa mãn x>0 và y>0

\(x+y+z=1\Rightarrow z=1-x-y\)Thay vào A ta được:
\(A=2xy+3y\left(1-x-y\right)+4\left(1-x-y\right)x\)
\(\Leftrightarrow2xy+3y-3xy-3y^2+4x-4x^2-4xy-A=0\)
\(\Leftrightarrow3y-3y^2+4x-4x^2-5xy-A=0\)
\(\Leftrightarrow-4x^2-\left(5y-4\right)x-3y^2+3y-A=0\)
\(\Leftrightarrow4x^2+\left(5y-4\right)x+3y^2-3y+A=0\)
\(\Delta=\left(5y-4\right)^2-16\left(3y^2-3y+A\right)\)
Để pt có nghiệm \(\Leftrightarrow\Delta\ge0\)
\(\Leftrightarrow\left(5y-4\right)^2-16\left(3y^2-3y+A\right)\ge0\)
\(\Leftrightarrow25y^2-40y+16-48y^2+48y-16A\ge0\)
\(\Leftrightarrow-23y^2+8y+16\ge16A\)
\(\Leftrightarrow16A\le-23\left(y^2-\frac{8}{23}y-\frac{12}{23}\right)=-23\left(y-\frac{4}{23}\right)^2+\frac{384}{23}\le\frac{384}{23}\)
\(\Rightarrow A\le\frac{24}{23}\)
Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}2xy+3y\left(1-x-y\right)+4\left(1-x-y\right)x=\frac{24}{23}\\\left(y-\frac{4}{23}\right)^2=0\\x+y+z=1\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=\frac{9}{23}\\y=\frac{4}{23}\\z=\frac{10}{23}\end{cases}}\)
Vậy Max A = \(\frac{24}{23}\)\(\Leftrightarrow\hept{\begin{cases}x=\frac{9}{23}\\y=\frac{4}{23}\\z=\frac{10}{23}\end{cases}}\)