
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, \(\left(2-x\right)\left(x+3\right)>0\Leftrightarrow\left(x-2\right)\left(x+3\right)< 0\)
Vì \(x+3>x-2\)
nên \(\hept{\begin{cases}x+3>0\\x-2< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>-3\\x< 2\end{cases}\Leftrightarrow-3< x< 2}\)
c, \(\left(5-2x\right)\left(x+4\right)>0\)
TH1 : \(\hept{\begin{cases}5-2x>0\\x+4>0\end{cases}}\Leftrightarrow\hept{\begin{cases}x< \frac{5}{2}\\x>-4\end{cases}}\Leftrightarrow-4< x< \frac{5}{2}\)
TH2 : \(\hept{\begin{cases}5-2x< 0\\x+4< 0\end{cases}}\Leftrightarrow\hept{\begin{cases}x>\frac{5}{2}\\x< -4\end{cases}}\)( vô lí )
bạn làm tương tự nhé

a, \(\left(5x-1\right)\left(2x-\frac{1}{3}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}5x-1=0\\2x-\frac{1}{3}=0\end{cases}\Rightarrow}\orbr{\begin{cases}5x=1\\2x=\frac{1}{3}\end{cases}\Rightarrow}\orbr{\begin{cases}x=\frac{1}{5}\\x=\frac{1}{6}\end{cases}}\)
b. \(\left(x^2+1\right)\left(x-4\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x^2+1=0\\x-4=0\end{cases}\Rightarrow}\orbr{\begin{cases}x^2=-1\left(Voly\right)\\x=4\end{cases}\Rightarrow x=4}\)
c, \(2x^2-\frac{1}{3}x=0\)
\(\Leftrightarrow x\left(2x-\frac{1}{3}\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\2x-\frac{1}{3}=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{6}\end{cases}}\)
d, \(\left(\frac{4}{5}\right)^{5x}=\left(\frac{4}{5}\right)^7\)
\(\Rightarrow5x=7\)
\(\Rightarrow x=\frac{7}{5}\)
e, Ta có: \(A=\frac{x+5}{x-2}=\frac{\left(x-2\right)+7}{x-2}=1+\frac{7}{x-2}\)
Để A ∈ Z <=> (x - 2) ∈ Ư(7) = { ±1; ±7 }
| x - 2 | 1 | -1 | 7 | -7 |
| x | 3 | 1 | 9 | -5 |
Vậy....
a) \(\left(5x-1\right)\left(2x-\frac{1}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}5x-1=0\\2x-\frac{1}{3}=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}5x=1\\2x=\frac{1}{3}\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=\frac{1}{5}\\x=\frac{1}{6}\end{cases}}\)
Vậy : ....
b) \(\left(x^2+1\right)\left(x-4\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+1=0\\x-4=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x^2=-1\left(loại\right)\\x=4\end{cases}}\)
c) \(2x^2-\frac{1}{3}x=0\)
\(\Leftrightarrow x\left(2x-\frac{1}{3}\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\2x-\frac{1}{3}=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x=\frac{1}{6}\end{cases}}\)
Vậy :...

`#3107.101107`
`1/2x + 4/5 = 2x - 8/5`
`=> 1/2x - 2x = -4/5 - 8/5`
`=> -3/2x = -12/5`
`=> x = -12/5 \div (-3/2)`
`=> x = 8/5`
Vậy, `x = 8/5`
_____
`\sqrt{x} = 5`
`=> x = 5^2`
`=> x = 25`
Vậy, `x = 25`
___
`x^2 = 3`
`=> x^2 = (+-\sqrt{3})^2`
`=> x = +- \sqrt{3}`
Vậy, `x \in {-\sqrt{3}; \sqrt{3}}.`

Lời giải:
1.
$|4-x|\geq 0$ với mọi $x$
$|2y+1|\geq 0$ với mọi $y$
Do đó để $|4-x|+|2y+1|=0$ thì $|4-x|=|2y+1|=0$
$\Leftrightarrow x=4; y=\frac{-1}{2}$
2.
$|x-3|=|5-2x|$
$\Leftrightarrow x-3=5-2x$ hoặc $x-3=2x-5$
$\Leftrightarrow x=\frac{8}{3}$ hoặc $x=2$
1 ) | 4 - x | + | 2y +1 | = 0
| Trường hợp 1 | Trường hợp 2 |
| x+1=0 | 2y-4=0 |
| x=0-1 | 2y=0+4 |
| x=-1 | 2y=2=>y=2 |

\(\left(2x+\frac{1}{2}\right)\left(\frac{4}{5}-x\right)=0\)
\(\Rightarrow\orbr{\begin{cases}2x+\frac{1}{2}=0\\\frac{4}{5}-x=0\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}2x=-\frac{1}{2}\\x=\frac{4}{5}\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=-\frac{1}{4}\\x=\frac{4}{5}\end{cases}}\)
Vậy,,,,,
\(\left(2x+\frac{1}{2}\right)\left(\frac{4}{5}-x\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}2x+\frac{1}{2}=0\\\frac{4}{5}-x=0\end{cases}\Leftrightarrow\orbr{\begin{cases}2x=\frac{-1}{2}\\x=\frac{4}{5}\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=\frac{-1}{4}\\x=\frac{4}{5}\end{cases}}}\)
Vậy \(x=\frac{-1}{4};x=\frac{4}{5}\)

|5\(x\) - 4| = |\(x+2\)|
\(\left[{}\begin{matrix}5x-4=x+2\\5x-4=-x-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}4x=6\\6x=2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{1}{3}\end{matrix}\right.\)
vậy \(x\in\) { \(\dfrac{1}{3};\dfrac{3}{2}\)}
|2\(x\) - 3| - |3\(x\) + 2| = 0
|2\(x\) - 3| = | 3\(x\) + 2|
\(\left[{}\begin{matrix}2x-3=3x+2\\2x-3=-3x-2\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-5\\x=\dfrac{1}{5}\end{matrix}\right.\)
vậy \(x\in\){ -5; \(\dfrac{1}{5}\)}

\(x.\left(x-\frac{1}{7}\right)\left(\frac{1}{9}+x\right)< 0\)
có 4 TH ( Trường hợp)
TH1: \(\hept{\begin{cases}x>0\\x-\frac{1}{7}>0\\\frac{1}{9}+x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\x>\frac{1}{7}\\x< -\frac{1}{9}\end{cases}}}\)( vô lí)
TH2:\(\hept{\begin{cases}x>0\\x-\frac{1}{7}< 0\\\frac{1}{9}+x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x>0\\x< \frac{1}{7}\\x>-\frac{1}{9}\end{cases}\Leftrightarrow}0< x< \frac{1}{7}}\)
TH3:\(\hept{\begin{cases}x< 0\\x-\frac{1}{7}>0\\\frac{1}{9}+x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 0\\x>\frac{1}{7}\\x>-\frac{1}{9}\end{cases}}}\)(vô lí )
TH4:\(\hept{\begin{cases}x< 0\\x+\frac{1}{7}< 0\\\frac{1}{9}-x< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x< 0\\x< -\frac{1}{7}\\x>\frac{1}{9}\end{cases}}}\)(vô lí)
KL: 0<x<1/7
b) \(\frac{\left(4-x\right)}{2x}-\frac{1}{5}>0\)đk: \(x\ne0\)
<=> \(\left(4-x\right).5-2x.1>0\)
<=> \(20-5x-2x>0\)
<=> \(20-7x>0\)
<=> \(20>7x\Leftrightarrow x< \frac{20}{7}\)

a, \(\left|x^2+2x\right|+\left|\left(x+2\right)\left(x-7\right)\right|=0\)
Dấu ''='' xảy ra khi : \(x^2+2x=0\)và \(\left(x+2\right)\left(x-7\right)=0\)
\(\Leftrightarrow x=0or-2andx=-2;7\)
Vậy \(x\in\left\{0;-2;7\right\}\)
b, tương tự

Vì : \(\left(2x-5\right)^{2022}\ge0\forall x,\left(3y+4\right)^{2024}\ge0\forall y\\ =>\left(2x-5\right)^{2022}+\left(3y+4\right)^{2024}\ge0\)
Do đó đề bài xảy ra khi và chỉ khi :
\(\left\{{}\begin{matrix}\left(2x-5\right)^{2022}=0\\\left(3y+4\right)^{2024}=0\end{matrix}\right.\\ =>\left(x;y\right)=\left(\dfrac{5}{2};-\dfrac{4}{3}\right)\)
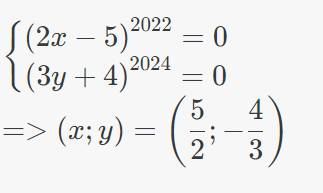 Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Mình ko biết cách để làm ra đc kết quả này, có thể giải thích cụ thể hơn ko ạ?
Ta có : \(\left|2x-4\right|>0\)
Để \(\left(x+5\right)\left|2x-4\right|< 0\)
Thì \(\left(x+5\right)< 0\)
\(\Leftrightarrow x< -5\)
còn cách x= 2 nữa thiếu zùi