Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


y = ax + b ⇒ y′ = a và dy = adx = aΔx;
Δy = a(x + Δx) + b − [ax + b] = aΔx..
Vậy dy = Δy.


a.
\(\Leftrightarrow m-cosx\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\ge max\left(cosx\right)\)
\(\Leftrightarrow m\ge1\)
b.
\(\Leftrightarrow2sinx-m\ge0\) ; \(\forall x\)
\(\Leftrightarrow m\le2sinx\) ; \(\forall x\)
\(\Leftrightarrow m\le\min\limits_{x\in R}\left(2sinx\right)\)
\(\Leftrightarrow m\le-2\)
c.
\(\Leftrightarrow cosx+m\ne0\) ; \(\forall x\)
\(\Leftrightarrow\left[{}\begin{matrix}m>\max\limits_R\left(cosx\right)\\m< \min\limits_R\left(cosx\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)

a: ĐKXĐ: 2*sin x+1<>0
=>sin x<>-1/2
=>x<>-pi/6+k2pi và x<>7/6pi+k2pi
b: ĐKXĐ: \(\dfrac{1+cosx}{2-cosx}>=0\)
mà 1+cosx>=0
nên 2-cosx>=0
=>cosx<=2(luôn đúng)
c ĐKXĐ: tan x>0
=>kpi<x<pi/2+kpi
d: ĐKXĐ: \(2\cdot cos\left(x-\dfrac{pi}{4}\right)-1< >0\)
=>cos(x-pi/4)<>1/2
=>x-pi/4<>pi/3+k2pi và x-pi/4<>-pi/3+k2pi
=>x<>7/12pi+k2pi và x<>-pi/12+k2pi
e: ĐKXĐ: x-pi/3<>pi/2+kpi và x+pi/4<>kpi
=>x<>5/6pi+kpi và x<>kpi-pi/4
f: ĐKXĐ: cos^2x-sin^2x<>0
=>cos2x<>0
=>2x<>pi/2+kpi
=>x<>pi/4+kpi/2
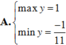
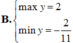
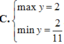
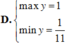
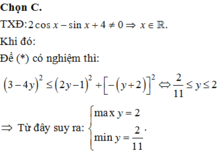
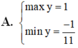
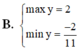
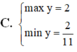
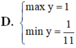
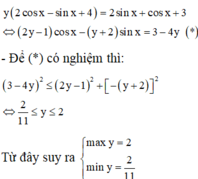
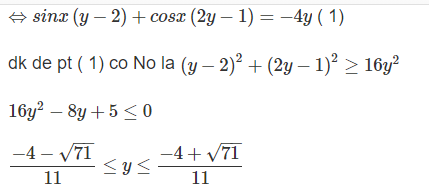
y’= sinx + xcosx – sinx = xcosx
do đó dy= xcosxdx
Đáp án là A