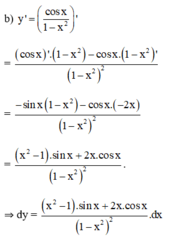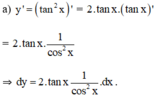Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


1.
\(y_{n+2}+2y_{n+1}+4y_n=3n-4\)
Xét phương trình thuần nhất: \(y_{n+2}+2y_{n+1}+4y_n=0\)
Pt đặc trưng: \(\lambda^2+2\lambda+4=0\Rightarrow\lambda_{1,2}=2\left(cos\frac{2\pi}{3}\pm sin\frac{2\pi}{3}\right)\)
\(\Rightarrow\) Nghiệm của pt thuần nhất có dạng:
\(\overline{y_n}=2^n\left(c_1.cos\frac{2n\pi}{3}+c_2.sin\frac{2n\pi}{3}\right)\)
Tìm nghiệm riêng có dạng: \(y_n^0=an+b\)
Thay vào pt:
\(a\left(n+2\right)+b+2\left[a\left(n+1\right)+b\right]+4\left[an+b\right]=3n-4\)
\(\Leftrightarrow7an+4a+7b=3n-4\)
\(\Rightarrow\left\{{}\begin{matrix}7a=3\\4a+7b=-4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}a=\frac{3}{7}\\b=-\frac{40}{49}\end{matrix}\right.\)
Nghiệm riêng có dạng: \(y_n^0=\frac{3}{7}n-\frac{40}{49}\)
Nghiệm tổng quát: \(y_n=2^n\left(c_1.cos\frac{2n\pi}{3}+c_2.sin\frac{2n\pi}{3}\right)+\frac{3}{7}n-\frac{40}{49}\)
2.
\(\left(y^2-2\right)dx=y\left(x^2+1\right)dy\)
\(\Leftrightarrow\frac{y}{y^2-2}dy-\frac{1}{x^2+1}dx=0\)
Lấy tích phân 2 vế:
\(\Rightarrow\int\frac{y}{y^2-2}dy-\int\frac{1}{x^2+1}dx=C\)
\(\Rightarrow\frac{1}{2}ln\left|y^2-2\right|-arctanx=C\)

Mọi người không thích giúp đỡ, chỉ muốn lấy điểm, web học hiểu toán lại biến thành tựu trò chơi.
Đúng là mất thời gian, luống công mà.

a) \(dy=d\left(tan^2x\right)=\left(tan^2x\right)'dx=2tanx.\left(tanx\right)'dx=\dfrac{2tanx}{cosx}dx\)
b) \(dy=d\left(\dfrac{cosx}{1-x^2}\right)=\left(\dfrac{cosx}{1-x^2}\right)'dx=\dfrac{\left(cosx\right)'.\left(1-x^2\right)-cosx\left(1-x^2\right)'}{\left(1-x^2\right)^2}dx=\dfrac{\left(x^2-1\right).sinx+2xcosx}{\left(1-x^2\right)^2}=dx\)

y = ax + b ⇒ y′ = a và dy = adx = aΔx;
Δy = a(x + Δx) + b − [ax + b] = aΔx..
Vậy dy = Δy.