K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
NV
Nguyễn Việt Lâm
Giáo viên
1 tháng 9 2020
Câu đầu tìm m để ĐTHS làm sao bạn?
2.
\(x=1\) là TCĐ của ĐTHS \(\frac{mx^2-3x}{x-1}=0\) khi và chỉ khi \(mx^2-3x=0\) không có nghiệm \(x=1\)
\(\Leftrightarrow m.1^2-3.1\ne0\Leftrightarrow m\ne3\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 9 2021
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
NH
1
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
\(y'=3\left(m-1\right)x^2-6x-\left(m+1\right)\)
Hàm có cực đại và cực tiểu khi và chỉ khi \(y'=0\) có 2 nghiệm pb
\(\Leftrightarrow\left\{{}\begin{matrix}3\left(m-1\right)\ne0\\\Delta'=9+3\left(m-1\right)\left(m+1\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne1\\m^2>-2\left(\text{luôn đúng}\right)\end{matrix}\right.\)
Vậy \(m\ne1\)
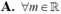
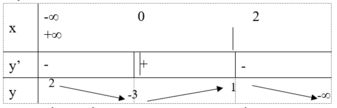
\(y=\dfrac{x^2-3x+1}{x-2}\)
\(D=R\ne\left\{2\right\}\)
\(\lim\limits_{x\rightarrow2^+}y=\dfrac{-1}{0^+}=-\infty\)
Vậy TCĐ của HS là: x=2
Hoặc cách khác:
Xét mẫu bằng 0 với giá trị đó nếu tử khác 0 => Là TCĐ
nếu tử bằng 0 => HS không có TCĐ
.
\(y=\dfrac{x^2-3x+1}{x-2}=\dfrac{x\left(x-2\right)-\left(x-2\right)-1}{x-2}=x-1-\dfrac{1}{x-2}\)
Ta thấy: \(\lim\limits_{x\rightarrow+\infty}\left[y-\left(x-1\right)\right]=\lim\limits_{x\rightarrow+\infty}-\dfrac{1}{x-2}=0\)
Vậy: y=x-1 là TCX của HS