H
3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
13 tháng 3 2023
x/y=3/4
=>x/3=y/4
=>x/15=y/20
y/z=5/7
=>y/5=z/7
=>y/20=z/28
=>x/15=y/20=z/28=(2x+3y-z)/(2*15+3*20-28)=186/62=3
=>x=45; y=60; z=84
NC
0
9 tháng 8 2023
\(\dfrac{x}{9}< \dfrac{4}{7}< \dfrac{x+1}{9}\)
=>\(\dfrac{7x}{63}< \dfrac{36}{63}< \dfrac{7x+7}{63}\)
\(\Rightarrow7x< 36< 7x+7\)
\(\Rightarrow x< \dfrac{36}{7}< x+1\)
\(\Rightarrow x< 5\dfrac{1}{7}< x+1\)
\(\Rightarrow x=5\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 8 2023
\(\dfrac{x}{9}\) < \(\dfrac{4}{7}\) < \(x\) + \(\dfrac{1}{9}\)
\(\dfrac{7x}{63}\) < \(\dfrac{36}{63}\) < \(\dfrac{63x}{63}\) + \(\dfrac{7}{63}\)
7\(x\) < 36 < 63\(x\) + 7
⇒\(\left\{{}\begin{matrix}7x< 36\\63x+7>36\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\63x>36-7\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\63x>29\end{matrix}\right.\)⇒\(\left\{{}\begin{matrix}x< \dfrac{36}{7}\\x>\dfrac{29}{63}\end{matrix}\right.\)
\(\dfrac{29}{63}\)< \(x\) < \(\dfrac{36}{7}\) vì \(x\in\) Z nên \(x\in\) { 1; 2; 3; 4; 5}
⇒ \(\dfrac{x}{9}\) = \(\dfrac{1}{9}\); \(\dfrac{2}{9}\); \(\dfrac{3}{9}\); \(\dfrac{4}{9}\);\(\dfrac{5}{9}\)
2 tháng 8 2017
a) | 9 + 7x | = 3 - 5x
\(\Rightarrow\orbr{\begin{cases}9+7x=3-5x\\9+7x=-\left(3-5x\right)\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}7x+5x=3-9\\9+7x=-3+5x\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}12x=-6\\7x-5x=-3-9\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{6}\\2x=-12\end{cases}}\)
\(\Rightarrow\orbr{\begin{cases}x=\frac{-1}{6}\\x=-6\end{cases}}\)
28 tháng 8 2021
Câu 4:
Ta có: \(\left|x+2\right|\ge0\forall x\)
\(\left|2y+3\right|\ge0\forall y\)
Do đó: \(\left|x+2\right|+\left|2y+3\right|\ge0\forall x,y\)
Dấu '='xảy ra khi x=-2 và \(y=-\dfrac{3}{2}\)
8 tháng 2 2023
Câu 11:
=>4,6x=6,21
=>x=1,35
12: \(A=-\left(1.4-x\right)^2-1.4< =-1.4\)
=>x=-1,4
Câu 9:
\(\Leftrightarrow\dfrac{10a+b}{100c+90+d}=\dfrac{1}{2}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{12}+...+\dfrac{1}{92}-\dfrac{1}{97}=\dfrac{1}{2}-\dfrac{1}{97}=\dfrac{95}{194}\)
=>a=9; b=5; c=1; d=4
=>a+b+c+d=9+5+1+4=19
TL
2
14 tháng 7 2023
=>(2x-1)^2=24^2
=>2x-1=24 hoặc 2x-1=-24
=>x=-23/2 hoặc x=25/2
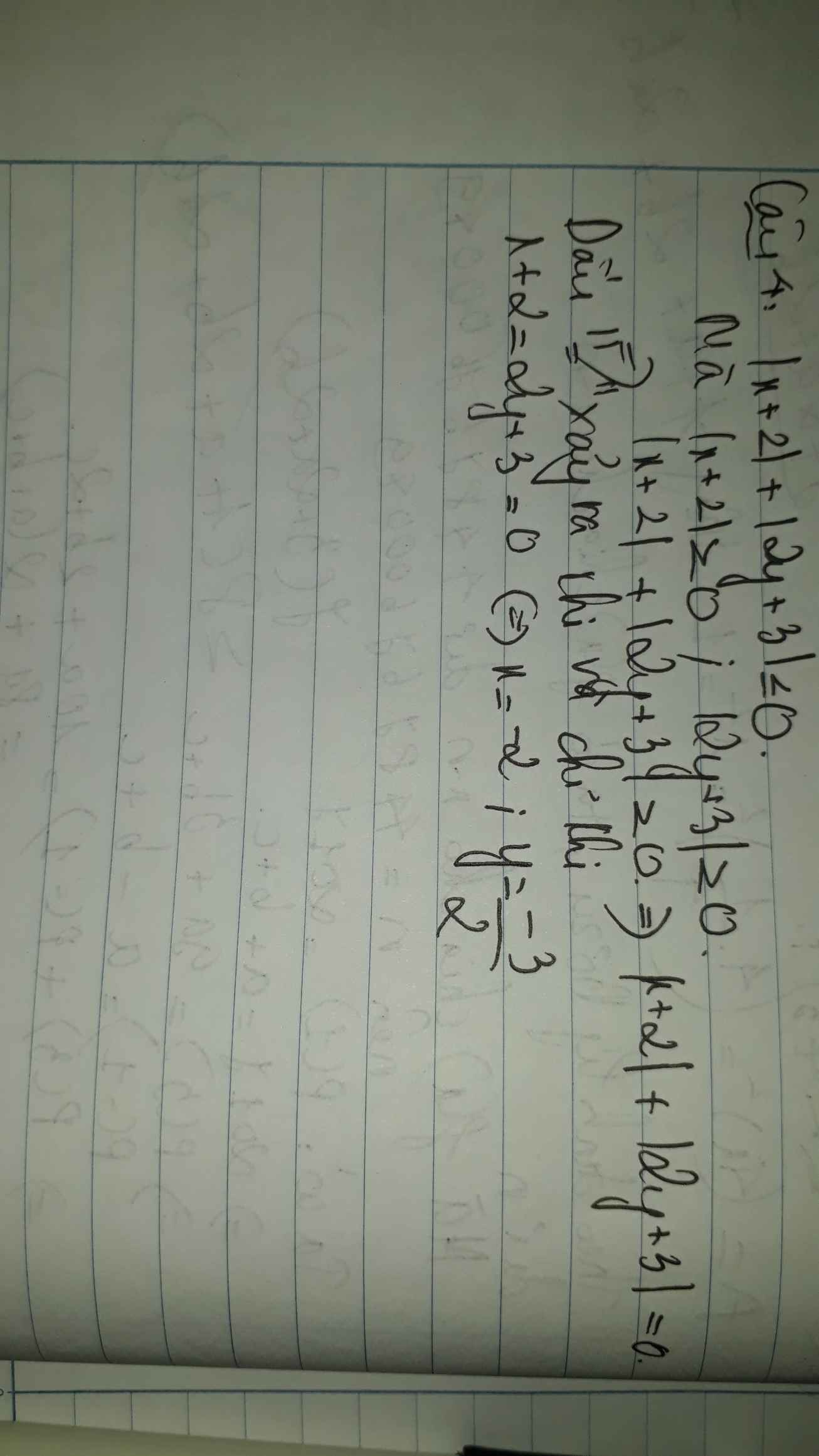
Ta có: A = |x - 2001| + |x - 1|
A = |x - 2001| + |1 - x| \(\ge\)|x - 2001 + 1 - x| = |-2000| = 2000
Dấu "=" xảy ra khi : x - 2001 + x - 1 = 0
<=> 2x - 2002 = 0
<=> 2x = 2002
<=> x = 1001
Vậy Min A = 2000 tại x = 1001