Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D.
Hàm số y = x 3 - 3 x 2 - 9 x + 1 xác định và liên tục trên R, nên trên đoạn [0;4] hàm số luôn xác định và liên tục.
Ta có: ![]()
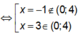
Khi đó: f(0) = 1; f(3) = -26; f(4) = -19
So sánh các giá trị trên ta được: ![]()
Suy ra: m + 2M = -26 + 2 = -24.
Vậy m + 2M = -24.

Chọn A
Xét hàm số y = x 3 - 3 x 2 trên đoạn [-2;1].
![]()
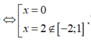
Ta có: ![]()
Do hàm số đã cho liên tục trên [-2;1] nên ![]()
Vậy T = M + m = -20.

Theo bài toán ta có thể suy ra BBT của đồ thị hàm số y = f (x) như sau:
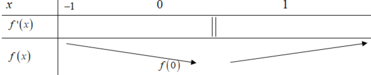
Dễ thấy trong các đáp án A, C, D đều sai. Hàm số đạt cực tiểu tại x = 0.
Chọn B

Chọn C.
Ta có: f ' x = 3 x 2 - 6 x ⇒ f ' x = 0
⇔ 3 x 2 - 6 x = 0
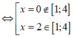
Lại có
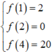
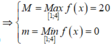
⇒ M + m = 20

Chọn B
Hàm số xác định và liên tục trên đoạn [1;4]. Đặt y = f(x)
Ta có: 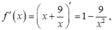
![]()
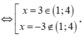
Có ![]()
![]()
Vậy m + M = 16.

Đáp án là A
Hàm số xác định và liên tục trên [0;3]
Ta có y' = 0 ⇔
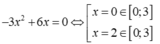
Khi đó y(0) = 2, y(2) = 6, y(3) = 2
Vậy M = 6; m = 2 => M + m = 8
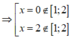
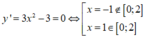
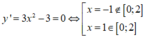

Đáp án A.
Hàm số liên tục trên đoạn [-4;4]
y' = 3x2 – 6x – 9, y’ = 0 => x2 – 2x – 3 = 0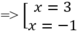
Ta có y(-4) = -41; y(4) = 15; y(-1) = 40; y(3) = 8
Vậy M = max[-4;4]y = 40 và m = min[-4;4]y = -41