Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đk: \(2011\le x\le2013\).
Với a,b >0 có: \(a+b\le\sqrt{2\left(a^2+b^2\right)}\)
<=> \(a^2+2ab+b^2\le2a^2+2b^2\)
<=> \(0\le a^2-2ab+b^2\)
<=> \(0\le\left(a-b\right)^2\) (luôn đúng)
Dấu "=" xảy ra <=>a=b>0
Áp dụng bđt trên có: \(\sqrt{x-2011}+\sqrt{2013-x}\le\sqrt{2\left(x-2011+2013-x\right)}\)
=> \(\frac{4026}{\sqrt{x-2011}+\sqrt{2013-x}}\ge\frac{4026}{\sqrt{2.2}}=2013\)
<=> \(Q\ge2013\)
Dấu "=" xảy ra <=>\(\sqrt{x-2011}=\sqrt{2013-x}\)
<=>x=2012(t/m)
Vậy minQ=2013 <=>x=2012

b)
https://hoc24.vn/cau-hoi/c-voi-a-b-c-la-cac-so-duong-thoa-man-dieu-kien-a-b-c-2-tim-max-q-sqrt2abcsqrt2bcasqrt2cab.8298826302
Bạn có thể tham khảo ở đây. Đừng quên like giúp mik nha bạn. Thx


Áp dụng bất đẳng thức AM - GM:
\(\dfrac{x^2}{y-1}+4\left(y-1\right)\ge2\sqrt{\dfrac{x^2}{y-1}.4\left(y-1\right)}\)
\(\Rightarrow\dfrac{x^2}{y-1}+4\left(y-1\right)\ge4x\).
Tương tự, \(\dfrac{y^2}{x-1}+4\left(x-1\right)\ge4y\).
Cộng vế với vế hai bđt trên rồi rút gọn ta được:
\(\dfrac{x^2}{y-1}+\dfrac{y^2}{x-1}\ge8\)
\(\Rightarrow P\ge8+2013=2021\).
Đẳng thức xảy ra khi x = y = 2.
Vậy....

Ta có: \(A=2013-xy\Leftrightarrow y=\frac{2013-A}{x}\)
Đặt \(2013-A=B\)thì ta có \(y=\frac{B}{x}\)(1)
Theo đề bài có
\(5x^2+\frac{y^2}{4}+\frac{1}{4x^2}=\frac{5}{2}\)
\(\Leftrightarrow5x^2+\frac{B^2}{4x^2}+\frac{1}{4x^2}=\frac{5}{2}\)
\(\Leftrightarrow20x^4-10x^2+B^2+1=0\)
Để PT có nghiệm (theo biến x2) thì \(\Delta\ge0\)
\(\Leftrightarrow5^2-20\left(B^2+1\right)\ge0\)
\(\Leftrightarrow B^2\le0,25\Leftrightarrow-0,5\le B\le0,5\)
\(\Leftrightarrow-0,5\le2013-A\le0,5\)
\(\Leftrightarrow2012,5\le A\le2013,5\)
Đạt GTLN khi \(\left(x,y\right)=\left(\frac{1}{2},-1;-\frac{1}{2},1\right)\)
Đạt GTNN khi \(\left(x;y\right)=\left(\frac{1}{2},1;-\frac{1}{2},-1\right)\)

\(M=\)như trên
\(=>M=4x^2-4x+1+x+\frac{1}{4x}+2010\)
\(=>M=\left(4x^2-4x+1\right)+\left(x+\frac{1}{4x}\right)+2010\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\)
Áp dụng BĐT Cô- si cho 2 số không âm, ta có:
\(x+\frac{1}{4x}\ge2\sqrt{x.\frac{1}{4x}}=2\sqrt{\frac{1}{4}}=1\)
\(=>M=\left(2x-1\right)^2+\left(x+\frac{1}{4x}\right)+2010\ge0+1+2010=2011\\ \)
=>minM=2011 khi x=\(\frac{1}{2}\)
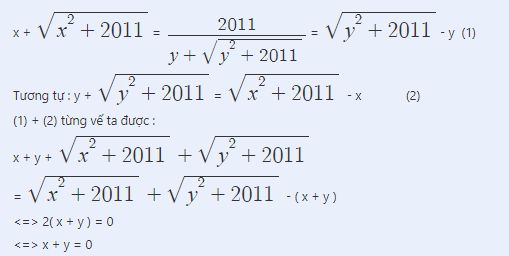
Ta có: \(A=\sqrt{2013-x}+\sqrt{x-2011}\ge\sqrt{2013-x+x-2011}=\sqrt{2}\)
Dấu "=" xảy ra khi \(\left[{}\begin{matrix}2013-x=0\\x-2011=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2013\\x=2011\end{matrix}\right.\)(thỏa mãn)
Vậy min A = \(\sqrt{2}\Leftrightarrow\)x = 2013 hoặc x = 2011
Mặt khác \(A^2\le\left(1^2+1^2\right)\left(2013-x+x-2011\right)=4\)
\(\Rightarrow A\le2\)
Vậy maxA=2 khi\(x=2012\)(thỏa mãn)