Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có x 2 - 6 x = x - 3 2 - 9 ≥ - 9 với mọi x.
x 2 - 6 x = - 9 ⇔ x - 3 = 0 ⇔ x = 3 ⇔ x = ± 3 .
Vậy giá trị nhỏ nhất của biểu thức với x ∈ ℝ là - 9 , đạt được khi x = ± 3 .

Ta có: x 2 ≥ 0 ; 3 x ≥ 0 ∀ x ⇒ g x = x 2 + 3 x ≥ 0 ∀ x
Do đó, giá trị nhỏ nhất của biểu thức g(x) là 0 khi x= 0.

Bạn tham khảo nhé!
Câu hỏi của Lê VĂn Chượng - Toán lớp 10 - Học toán với OnlineMath


Từ đề bài suy ra: 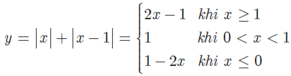
Bảng biến thiên
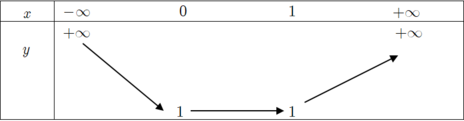
Ta có y(-2) =5; y(2) =3
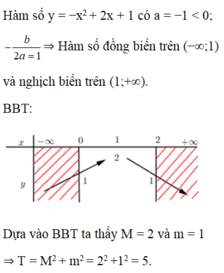
Dựa vào bảng biến thiên ta có

Chọn D.

\(\Delta=\left(m+1\right)^2-4\left(m^2-2m+2\right)=-3m^2+10m-7\ge0\)
\(\Rightarrow1\le m\le\dfrac{7}{3}\)
\(\left\{{}\begin{matrix}x_1+x_2=m+1\\x_1x_2=m^2-2m+2\end{matrix}\right.\)
\(P=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=\left(m+1\right)^2-2\left(m^2-2m+2\right)\)
\(=-m^2+6m-3\)
\(=\left(-m^2+6m-\dfrac{77}{9}\right)+\dfrac{50}{9}\)
\(=\left(\dfrac{11}{3}-m\right)\left(m-\dfrac{7}{3}\right)+\dfrac{50}{9}\le\dfrac{50}{9}\)
\(P_{max}=\dfrac{50}{9}\) khi \(m=\dfrac{7}{3}\)
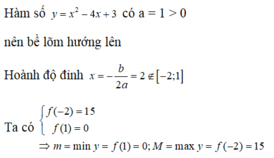


Đặt \(A=\frac{x^2+2}{x^2+x+2}\)
Ta có \(A\left(x^2+x+2\right)=x^2+2\Leftrightarrow x^2\left(A-1\right)+Ax+\left(2A-2\right)=0\)
Nếu A = 1 thì x = 0
Nếu \(A\ne1\) , Xét \(\Delta=A^2-4\left(A-1\right).\left(2A-2\right)=A^2-8\left(A-1\right)^2=-7A^2+16A-8\)
Để pt có nghiệm thì \(\Delta\ge0\Leftrightarrow-7A^2+16A-8\ge0\Rightarrow\frac{8-2\sqrt{2}}{7}\le A\le\frac{8+2\sqrt{2}}{7}\)
Từ đó tìm được giá trị lớn nhất và nhỏ nhất .
Cảm ơn bạn rất nhiều!