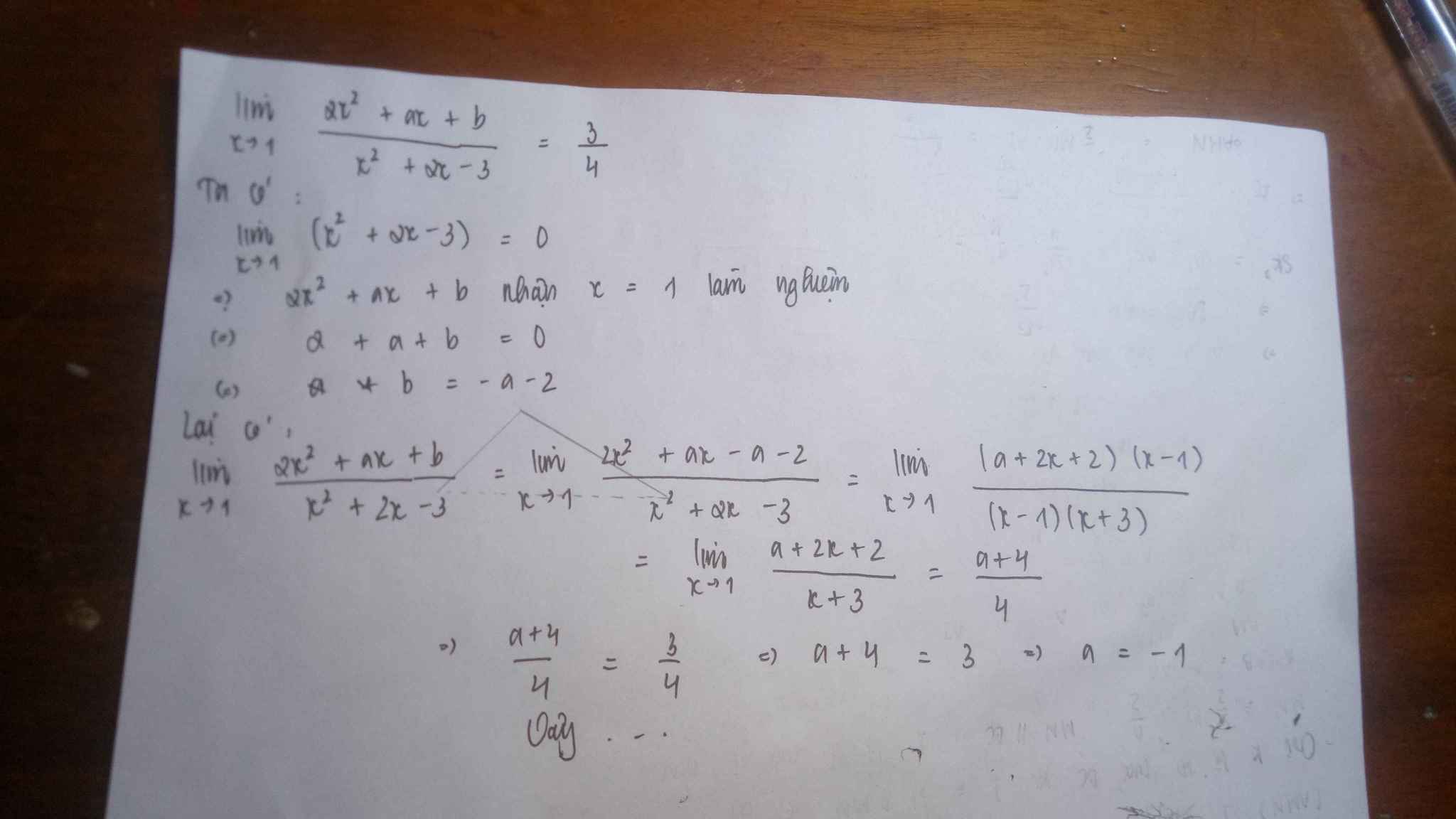Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giới hạn đã cho hữu hạn khi \(2x^2+ax+b=0\) có nghiệm \(x=1\)
\(\Rightarrow2+a+b=0\Rightarrow b=-a-2\)
Ta được: \(\lim\limits_{x\rightarrow1}\dfrac{2x^2+ax-a-2}{x^2-1}=\lim\limits_{x\rightarrow1}\dfrac{2\left(x-1\right)\left(x+1\right)+a\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2+a\right)}{\left(x-1\right)\left(x+1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2x+2+a}{x+1}\)
\(=\dfrac{4+a}{2}=\dfrac{1}{4}\)
\(\Rightarrow a=-\dfrac{7}{2}\Rightarrow b=\dfrac{3}{2}\)

\(x^2+2x-3=0\) có nghiệm \(x=1\) nên giới hạn đã cho hữu hạn khi \(2x^2+ax+b=0\) cũng có nghiệm \(x=1\)
\(\Rightarrow2.1^2+a.1+b=0\Rightarrow a+b+2=0\Rightarrow b=-a-2\)
Thay vào:
\(\lim\limits_{x\rightarrow1}\dfrac{2x^2+ax-a-2}{x^2+2x-3}=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2\right)+a\left(x-1\right)}{\left(x-1\right)\left(x+3\right)}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\left(x-1\right)\left(2x+2+a\right)}{\left(x-1\right)\left(x+3\right)}=\lim\limits_{x\rightarrow1}\dfrac{2x+2+a}{x+3}=\dfrac{4+a}{4}=\dfrac{3}{4}\)
\(\Rightarrow4+a=3\Rightarrow a=-1\Rightarrow b=-a-2=-1\)

đặt x^2+ax+b= (x-1)(x-m)
x^2+ax+b/x^2-1 = x-m/x+1
lim x-m/x+1=-1/2 suy ra 1-m/2=-1/2 nên m = 3
x^2+ax+b= (x-1)(x-3)=x^2-4x+3 suy ra a=-4, b=3

Tham khảo:
Vì hàm số có giới hạn hữu hạn tại x=1 nên biểu thức tử nhận x=1 làm nghiệm, hay 1+a+b=0.
Áp dụng vào giả thiết, được
\(^{lim}_{x\rightarrow1}\dfrac{x^2+ax-1-a}{x^2-1}=-\dfrac{1}{2}\Leftrightarrow^{lim}_{x\rightarrow1}\dfrac{\left(x-1\right)\left(x+1+a\right)}{\left(x-1\right)\left(x+1\right)}=-\dfrac{1}{2}\)
\(\Leftrightarrow^{lim}_{x\rightarrow1}\dfrac{x+1+a}{x+1}=-\dfrac{1}{2}\Leftrightarrow\dfrac{2+a}{2}=-\dfrac{1}{2}\Leftrightarrow a=-3\)
\(\Rightarrow b=2\)
Lời giải:
Vì $x^2-1\to 0$ khi $x\to 1$ nên để giới hạn đã cho hữu hạn thì $x^2+ax+b$ nhận $x=1$ là nghiệm
$\Leftrightarrow 1+a+b=0$
$\Leftrightarrow b=-a-1$
Khi đó:
\(\lim\limits_{x\to 1}\frac{x^2+ax+b}{x^2-1}=\lim\limits_{x\to 1}\frac{x^2+ax-a-1}{x^2-1}=\lim\limits_{x\to 1}\frac{(x-1)(x+1+a)}{(x-1)(x+1)}=\lim\limits_{x\to 1}\frac{x+a+1}{x+1}\)
\(=\frac{a+2}{2}=\frac{-1}{2}\Rightarrow a+2=-1\Rightarrow a=-3\)
$b=-a-1=3-1=2$

Giới hạn đã cho hữu hạn khi và chỉ khi \(b=1\)
Khi đó:
\(\lim\limits_{x\rightarrow+\infty}\left(\sqrt{x^2-ax+1}-x\right)=\lim\limits_{x\rightarrow+\infty}\dfrac{-ax+1}{\sqrt{x^2-ax+1}+x}\)
\(=\lim\limits_{x\rightarrow+\infty}\dfrac{-a+\dfrac{1}{x}}{\sqrt{1-\dfrac{a}{x}+\dfrac{1}{x^2}}+1}=-\dfrac{a}{2}\)
\(\Rightarrow-\dfrac{a}{2}=2\Rightarrow a=-4\)
Vậy \(\left(a;b\right)=\left(-4;1\right)\)

a/ \(=\lim\limits_{h\rightarrow0}\dfrac{2x^3+6x^2h+6xh^2+2h^3-2x^3}{h}\)
\(=\lim\limits_{h\rightarrow0}\dfrac{6xh^2+6x^2h+2h^3}{h}=\lim\limits_{h\rightarrow0}\left(6xh+6x^2+2h^2\right)=6x^2\)
b/ Xet day :\(S=x+x^2+....+x^{2021}\)
Day co \(\left\{{}\begin{matrix}u_1=x\\q=x\end{matrix}\right.\Rightarrow S=u_1.\dfrac{q^{2021}-1}{q-1}=x.\dfrac{x^{2021}-1}{x-1}\)
\(\Rightarrow\lim\limits_{x\rightarrow1}\dfrac{\dfrac{x^{2022}-x}{x-1}-2021}{x-1}=\lim\limits_{x\rightarrow1}\dfrac{x^{2022}-x-2021x+2021}{\left(x-1\right)^2}\)
\(=\lim\limits_{x\rightarrow1}\dfrac{\dfrac{x^{2022}}{x^2}-\dfrac{x}{x^2}-\dfrac{2021x}{x^2}+\dfrac{2021}{x^2}}{\dfrac{x^2}{x^2}-\dfrac{2x}{x^2}+\dfrac{1}{x^2}}=\lim\limits_{x\rightarrow1}\dfrac{x^{2020}}{1}=1\)
Lam lai cau b, hinh nhu bi nham sang dang \(\dfrac{\infty}{\infty}\) roi
Xet day: \(S=x+x^2+...+x^{2021}\)
\(\Rightarrow S=x.\dfrac{x^{2021}-1}{x-1}=\dfrac{x^{2022}-x}{x-1}\)
\(\Rightarrow\lim\limits_{x\rightarrow1}\dfrac{x^{2022}-2022x+2021}{\left(x-1\right)^2}\)
L'Hospital: \(\Rightarrow...=\lim\limits_{x\rightarrow1}\dfrac{2022x^{2021}-2022}{2\left(x-1\right)}=\lim\limits_{x\rightarrow1}\dfrac{2022.2021.x^{2020}}{2}=2043231\)
Is that true :v?

1/ \(\lim\limits_{x\rightarrow0^-}\left(\dfrac{x-2}{x^3}\right)=\lim\limits_{x\rightarrow0^-}\dfrac{2-x}{-x^3}=\dfrac{2}{0}=+\infty\)
2/ \(\lim\limits_{x\rightarrow1^+}\dfrac{\left(x^3-x^2\right)^{\dfrac{1}{2}}}{\left(x-1\right)^{\dfrac{1}{2}}+1-x}=\lim\limits_{x\rightarrow1^+}\dfrac{\dfrac{1}{2}\left(x^3-x^2\right)^{-\dfrac{1}{2}}.\left(3x^2-2x\right)}{\dfrac{1}{2}\left(x-1\right)^{-\dfrac{1}{2}}-1}=0\)
3/ \(\lim\limits_{x\rightarrow1^+}\dfrac{1-\left(x^2+x+1\right)}{x^3-1}=\dfrac{1-3}{0}=-\infty\)
4/ \(\lim\limits_{x\rightarrow-\infty}\left(-\infty-\sqrt[3]{1+\infty}\right)=-\left(\infty+\infty\right)=-\infty?\) Cái này ko chắc :v

Trình bày công thức các thứ khá dài nên tôi thử nói hướng, nếu bạn hiểu đc và làm đc thì ok còn nếu k hiểu thì bảo mình, mình làm full cho
Bây giờ phân tích mẫu trước, ra (x-1)2(x+2)
Để cái lim này nó ra đc 1 số thực thì tử và mẫu cùng phải triệt tiêu (x-1)2 đi, tức là tử phải chia hết (x-1)2, tức là tử cũng phải có nghiệm kép x=1
Do đó \(\left\{{}\begin{matrix}f\left(1\right)=0\\f'\left(1\right)=0\end{matrix}\right.\)