NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
7L
1
TC
4 tháng 4 2022
\(\dfrac{x}{4}=\dfrac{y}{4}=\dfrac{z}{5}=>\dfrac{2x^2}{32}=\dfrac{2y^2}{32}=\dfrac{3z^2}{75}\)
AD t/c của dãy tỉ số bằng nhâu ta có
\(\dfrac{2x^2}{32}=\dfrac{2y^2}{32}=\dfrac{3z^2}{75}=\dfrac{2x^2+2y^2-3z^2}{32+32-75}=\dfrac{-100}{-11}=\dfrac{100}{11}\)
\(=>\left[{}\begin{matrix}x=\dfrac{400}{11}\\y=\dfrac{400}{11}\\z=\dfrac{500}{11}\end{matrix}\right.\)
SO
0
DV
1
AH
Akai Haruma
Giáo viên
23 tháng 10 2023
Đoạn:
2x
2 + 2y
2 − 3z
2= -100 là như thế nào bạn nhỉ?
Bạn viết lại đề để mọi người hiểu hơn nhé.
LS
Tìm x,y,z biết :
a, x/y=7/3 và 5x-2y=87
b, 20x=15y=12z và 2x+y-z= 5
c, x-1/2=y-2/3=z-3/4 và x+3y-2z= 49
1
N
29 tháng 10 2018
\(\frac{x}{y}=\frac{7}{3}\Rightarrow\frac{x}{7}=\frac{y}{3}=\frac{5x}{35}=\frac{2y}{6}\)
áp dụng t/c dãy tỉ số bằng nhau ta có:
\(\frac{x}{7}=\frac{y}{3}=\frac{5x}{35}=\frac{2y}{6}=\frac{5x-2y}{35-6}=\frac{87}{29}=3\)
\(\frac{x}{7}=3\Rightarrow x=21\)
\(\frac{y}{3}=3\Rightarrow y=9\)
vậy x=21, y=9
b) \(20x=15y=12z=\frac{x}{\frac{1}{20}}=\frac{y}{\frac{1}{15}}=\frac{z}{\frac{1}{12}}=\frac{2x}{\frac{1}{40}}\)
áp dụng t/c dãy tí số bằng nhau ta có:
\(\frac{x}{\frac{1}{20}}=\frac{y}{\frac{1}{15}}=\frac{z}{\frac{1}{12}}=\frac{2x}{\frac{1}{40}}=\frac{2x+y-z}{\frac{1}{40}+\frac{1}{15}-\frac{1}{12}}=\frac{5}{\frac{1}{120}}=600\)
đến đây tự tính =)
23 tháng 7 2019
Ta có : 20x =15y =12z
\(=>\frac{20x}{60}=\frac{15y}{60}=\frac{12z}{60}\)(dạng này thì bạn tìm bội chung nhỏ nhất của mấy số 20,15,12 rồi lấy làm mẫu chung như vầy để rút gọn cho còn x,y,z là đc nha)
\(=>\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{2y}{8}=\frac{3z}{15}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=\frac{2y}{8}=\frac{3z}{15}=\frac{x+2y+3z}{3+8+15}=\frac{130}{26}=5\)
\(=>\hept{\begin{cases}x=5.3=15\\y=5.4=20\\z=5.5=25\end{cases}}\)
23 tháng 7 2019
20x = 15y = 12z => \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
áp dụng t/c dãy tỉ số bằng nhau:
\(\frac{x+2y+3z}{3+4.2+5.3}=\frac{130}{26}=5\)
=> x=15, y=20, z=25
LT
1
AH
Akai Haruma
Giáo viên
27 tháng 8
Lời giải:
Áp dụng TCDTSBN:
$\frac{12x-15y}{7}=\frac{20z-12x}{9}=\frac{15y-20z}{11}=\frac{12x-15y+20z-12x+15y-20z}{7+9+11}=\frac{0}{27}=0$
$\Rightarrow 12x=15y; 20z=12x$
$\Rightarrow 12x=15y=20z$
$\Rightarrow \frac{12x}{60}=\frac{15y}{60}=\frac{20z}{60}$
$\Rightarrow \frac{x}{5}=\frac{y}{4}=\frac{z}{3}$
Tiếp tục áp dụng TCDTSBN:
$\frac{x}{5}=\frac{y}{4}=\frac{z}{3}=\frac{x+y+z}{5+4+3}=\frac{96}{12}=8$
$\Rightarrow x=8.5=40; y=8.4=32; z=3.8=24$
MT
1
NL
0
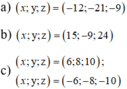
20x = 15y = 12z
\(\frac{20x}{60}=\frac{15y}{60}=\frac{12z}{60}\)
\(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}\)
Đặt \(\frac{x}{3}=\frac{y}{4}=\frac{z}{5}=k\)
\(\Rightarrow\hept{\begin{cases}x=3k\\y=4k\\z=5k\end{cases}}\)
Thay x , y , z vào biểu thức đề cho , ta có :
2x2 + 2y2 - 3z2 = -100
2.(3k)2 + 2.(4k)2 - 3.(5k)2 = -100
2.9k2 + 2.16k2 - 3.25k2 = -100
18k2 + 32k2 - 75k2 = -100
(18 + 32 - 75)k2 = -100
-25k2 = -100
k2 = 4
\(\Rightarrow\orbr{\begin{cases}k=2\\k=-2\end{cases}}\)
Với k = 2
\(\Rightarrow\hept{\begin{cases}x=3k=3.2=6\\y=4k=4.2=8\\z=5k=5.2=10\end{cases}}\)
Với k = -2
(tương tự như k = 2)