Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
● Cách 1 : Tìm các peptit dựa vào số mol các amino axit và tỉ lệ mol của các peptit
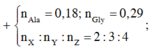
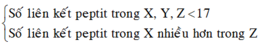


Tham khảo
Ta có: nGly = 0,8 mol; nAla = 0,9 mol; nVal = 1 mol
→ Số gốc Gly : Ala :Val = 0,8 : 0,9 : 1 = 8 : 9 : 10
Ta dùng phương pháp trùng ngưng hóa để giải bài toán này:
Đặt công thức của các peptit lần lượt là (X)a , (Y)b, (Z)c (a, b, c là độ dài peptit X, Y, Z)
2(X)a + 3(Y)b + 5(Z)c → (X)2a(Y)3b(Z)5c + 9H2O
(X)2a(Y)3b(Z)5c + H2O → Gly + Ala + Val
0,8 0,9 1,0 mol
8 9 10
Ta có: a + b + c = 6 + 3 = 9
Mặt khác: (8 + 9 + 10).k = 2a + 3b + 5c
Mà a, b, c khác nhau nên a, b,c có thể là 2, 3, 4
Ta có: 2.4 + 3.3 + 5.2 ≤ 27k ≤ 2.2 + 3.3 + 5.4
→ 1 ≤ k ≤ 1,222
Mà k là số tự nhiên nên k = 1
Ta có:
2(X)a + 3(Y)b + 5(Z)c → (X)2a(Y)3b(Z)5c + 9H2O
0,1 → 0,9 mol
(Xa)2 (Yb)3 (Zc)5+ 26H2O → 8 Gly + 9Ala + 10Val
0,1 2,6 ← 0,8 0,9 1,0 mol
Theo bảo toàn khối lượng ta có: m + 2,6.18 = 0,9.18 + 60 + 80,1 + 117 → m = 226,5 gam
Cách 2:
Ta có: nGly = 0,8 mol; nAla = 0,9 mol; nVal = 1 mol
Ta có thể sắp xếp các ɑ-aminoaxit vào 3 peptit A, B, C sao cho thỏa mãn đề bài như sau:
A (Val-Ala-Ala-Ala): 0,2 mol
B (Val-Gly-Ala): 0,3 mol
C (Val-Gly): 0,5 mol
Vậy m = 0,2.(117 + 89.3 - 18.3) + 0,3.(117 + 75 + 89 - 18.2) + 0,5.(117 + 75 - 18) = 226,5 gam

Dễ thấy cả 2 axit đều có 2 H => HCOOH và HCOO - COOH
Đặt số mol 2 chất là x và y,đặt a = 1 thì
x + y = 1
x + 2y = 1,4
=> x = 0,6 ; y = 0,4
=> %mHCOOH = 43,4%

Đáp án A
![]()
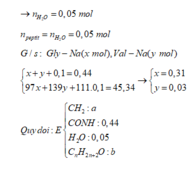
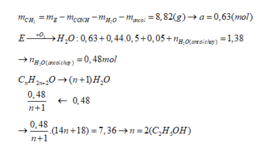
=> neste = nancol = 7,36:46 = 0,16 mol. Ta thấy chỉ có nGly-Na > neste nên este là este của Gly (Gly-C2H5)
nN(peptit) = 0,44 – 0,16 = 0,28 mol
=> Y là pentapeptit (c mol), Z là hexapeptit (d mol)


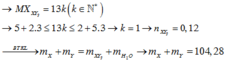
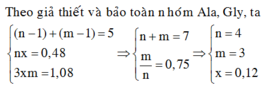
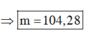
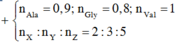

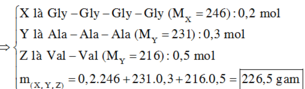
Đáp án B
Vì thủy phân cho cùng 1 lượng α – amino axit nhưng mY < mZ
⇒ Số liên kết peptit trong Y > Số liên kết peptit trong Z
Đặt số liên kết peptit Y = a||⇒ Số liên kết peptit trong Z = (a–1)
Ta có: Y + aH2O → (a+1) amino axit X (1) ||⇒ nH2O (1) = 1,12a/(a+1)
Ta có: Z + (a–1)H2O → a mol amino axit X (2) ||⇒ nH2O (2) = 1,12×(a–1)/a
[Mấu chốt] Vì khối lượng α – amino axit được sinh ra ở cả 2 trường hợp là như nhau
Nên áp dụng định luật BTKL ta có: mY + nH2O (1) = mZ + nH2O (2)
⟺ 83,552 + 18×1,12a/(a+1) = 84,56 + 18×1,12×(a–1)/a ||⇒ a = 4