Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x(x – y) + y(x + y)
= x.x – x.y + y.x + y.y
= x2 – xy + xy + y2
= x2 + y2.
Tại x = –6 ; y = 8, giá trị biểu thức bằng : (–6)2 + 82 = 36 + 64 = 100.

a: \(x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2\)
=100
b: \(x\left(x^2-y\right)-x^2\left(x+y\right)+y\left(x^2-x\right)\)
\(=x^3-xy-x^3-x^2y+x^2y-xy\)
\(=-2xy\)

a) x(x – y) + y (x + y) = x2 – xy +yx + y2= x2+ y2
với x = -6, y = 8 biểu thức có giá trị là (-6)2 + 82 = 36 + 64 = 100

x.(x2 – y) – x2.(x + y) + y.(x2 – x)
= x.x2 – x.y – (x2.x + x2.y) + y.x2 – y.x
= x3 – xy – x3 – x2y + x2y – xy
= (x3 – x3) + (x2y – x2y) – xy – xy
= –2xy
Tại 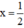 và y = –100, giá trị biểu thức bằng:
và y = –100, giá trị biểu thức bằng: 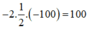

x(x - y) + y(x + y)
= x.x + x.(-y) + y.x + y.y
= x2 - xy + xy + y2
= x2 + y2 (1)
Thay x = -6 và y = 8 vào (1), ta có:
x2 + y2 = (-6)2 + 82 = 100
Vậy:...
\(A,x\left(x-y\right)+y\left(x+y\right)\)
\(=x^2-xy+xy+y^2\)
\(=x^2+y^2=\left(-6\right)^2+8^2\)
\(=36+64=100\)

Ta có:\(x\left(x+y\right)+y\left(x-y\right)=x^2+xy+xy-y^2\)
\(=x^2+2xy-y^2\)
\(=-\left(x^2-2xy+y^2\right)+2x^2\)
Áp dụng hằng đẳng thức (a-b)2=a2-2ab+b2 ta đc:
\(=2x^2-\left(x-y\right)^2\)
Tại x = - 8 ; y = 7 ta đc:
\(=2\left(-8\right)^2-\left(-8-7\right)^2\)
\(=-241\)

x(x2 – y) – x2 (x + y) + y (x2– x) = x3 – xy – x3 – x2y + yx2 – yx= (2x-2y) – (x2 -2xy +y2) =2(x-y) – (x-y)2
Với x =1/2, y = -100 biểu thức có giá trị là -2 . 1/2. (-100) = 100.

x(x2 – y) – x2 (x + y) + y (x2– x) = x3 – xy – x3 – x2y + yx2 – yx= (2x-2y) – (x2 -2xy +y2) =2(x-y) – (x-y)2
Với x =1/2, y = -100 biểu thức có giá trị là -2 . 1/2. (-100) = 100.
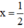 và y = –100;
và y = –100;
Mik ko ấn vào xem dc bn ơi, onl math nói câu trả lời đó chứa từ ngữ ko phù hợp
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)