K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
QT
2
GL
21 tháng 9 2023
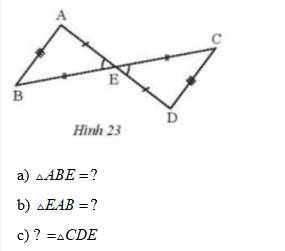
a) Tam giác ABE = tam giác DCE
b) Tam giác EAB = tam giác ECD
C) Tam giác ABE = tam giác CDE
HQ
Hà Quang Minh
Giáo viên
21 tháng 9 2023
\(a,\Delta ABE=\Delta DCE\\ b,\Delta EAB=\Delta ECD\\ c,\Delta BAE=\Delta CDE\)
PT
1
CM
14 tháng 7 2018
Vì x và y là hai đại lượng tỉ lệ nghịch nên xy = a (với a là một số khác 0).
Khi x = 2, y = 15 ⇒ a = xy = 30
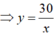
Vì x và y là hai đại lượng tỉ lệ nghịch nên:
x1.y1 = x2.y2 = x3. y3 = x4.y4 = 30.
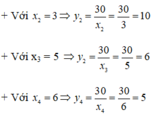
Kết quả như sau:
| x1 = 2 | x2 = 3 | x3 = 5 | x4 = 6 |
| y1 = 15 | y2 = 10 | y3 = 6 | y4 = 5 |
| x1y1 = 30 | x2y2 = 30 | x3y3 = 30 | x4y4 = 30 |
18 tháng 9 2023
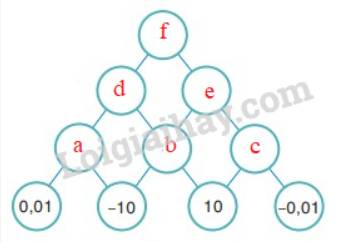
Theo quy luật bài cho, ta được:
a = 0,01 . (-10) = -0,1
b = (-10) . 10 = -100
c = 10 . (-0,01) = -0,1
d = a.b = (-0,1) . (-100) = 10
e = b.c = (-100) . (-0,1) = 10
f = d.e = 10 . 10 = 100
Như vậy:
28 tháng 11 2021
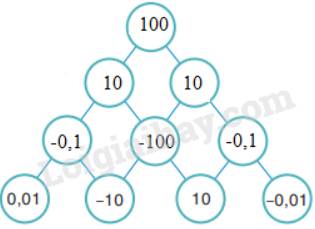
a/
Vì z và y là 2 đại lượng tỉ lệ nghịch nên
=>x.y=a
=>2.30=a
=>a=60
Vậy x và y tỉ lệ nghịch với nhau theo hệ số tỉ lệ là 60.
b/
y2=20
y3=15
y4=12
CM
6 tháng 6 2017
| x | X1 = 2 | X2 = 3 | X3 = 4 | X4 = 5 |
| y | Y1 = 30 | Y2 = 20 | Y3 = 15 | Y4 = 12 |
CM
20 tháng 2 2017
| x | X1 = 3 | X2 = 4 | X3 = 5 | X4 = 6 |
| y | Y1 = 6 | Y2 = 8 | Y3 = 10 | Y4 = 12 |
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a)\({\left[ {{{\left( {\frac{{ - 2}}{3}} \right)}^2}} \right]^5} = {\left( {\frac{{ - 2}}{3}} \right)^{2.5}} = {\left( {\frac{{ - 2}}{3}} \right)^{10}}\)
Vậy dấu “?” bằng 10.
b) \({\left[ {{{\left( {0,4} \right)}^3}} \right]^3} = {\left( {0,4} \right)^{3.3}} = {\left( {0,4} \right)^9}\)
Vậy dấu “?” bằng 9.
c) \({\left[ {{{\left( {7,31} \right)}^3}} \right]^0} = 1\)
Vậy dấu “?” bằng 1.
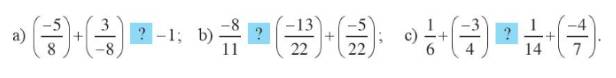
a)\(\left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{3}{{ - 8}}} \right) = \left( {\frac{{ - 5}}{8}} \right) + \left( {\frac{{ - 3}}{8}} \right) = - 1\)
Vậy dấu cần điền là “=”.
b)\(\left( {\frac{{ - 13}}{{22}}} \right) + \left( {\frac{{ - 5}}{{22}}} \right) = \frac{{ - 18}}{{22}} = \frac{{ - 9}}{{11}} < \frac{{ - 8}}{{11}}\).
Vậy dấu cần điền là “>”.
c) \(\frac{1}{6} + \left( {\frac{{ - 3}}{4}} \right) = \frac{2}{{12}} + \left( {\frac{{ - 9}}{{12}}} \right) = \frac{{ - 7}}{{12}}\)
\(\frac{1}{{14}} + \left( {\frac{{ - 4}}{7}} \right) = \frac{1}{{14}} + \left( {\frac{{ - 8}}{{14}}} \right) = \frac{{ - 7}}{{14}}\)
Mà 12 < 14 nên \(\frac{{ 7}}{{12}} > \frac{{ 7}}{{14}}\), do đó \(\frac{{ - 7}}{{12}} < \frac{{ - 7}}{{14}}\)
Vậy dấu cần điền là “<”.