Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔANP và ΔBPN có
AN=BP
\(\widehat{ANP}=\widehat{BPN}\)
PN chung
Do đó: ΔANP=ΔBPN
b: Xét ΔINP có \(\widehat{INP}=\widehat{IPN}\)
nên ΔINP cân tại I
=>IN=IP
mà MN=MP
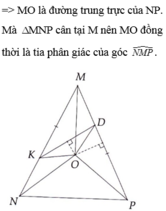
nên MI là đường trung trực của NP(1)
c: Xét ΔMNH vuông tại N và ΔMPH vuông tại P có
MH chung
MN=MP
Do đó: ΔMNH=ΔMPH
Suy ra: HN=HP
hay H nằm trên đường trung trực của NP(3)
Từ (1)và (3) suy ra M,I,H thẳng hàng

a: Xét ΔPAN có
PM vừa là đường cao, vừa là trung tuyến
=>ΔPAN cân tại P
b: \(PM=\sqrt{5^2-4^2}=3\left(cm\right)\)
Xét ΔPAN có
NB,PM là trung tuyến
NB cắt PM tại G
=>G là trọng tâm
GP=2/3*3=2cm
c: CI là trung trực của MP
=>I là trung điểm của MP và CI vuông góc MP tại I
Xét ΔMPN có
I là trung điểm của PM
IC//MN
=>C là trung điểm của PN
=>PM,NB,AC đồng quy

a) Xét ΔBNP có
BA là đường trung trực ứng với cạnh PN(gt)
nên ΔBNP cân tại B(Định lí tam giác cân)
b) Xét ΔMBN vuông tại M và ΔCBP vuông tại C có
BN=BP(cmt)
\(\widehat{MBN}=\widehat{CBP}\)(hai góc đối đỉnh)
Do đó: ΔMBN=ΔCBP(cạnh huyền-góc nhọn)

Mình sẽ cho người nào trả lời nhanh nhất