
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Số tập con của tập A gồm n phần tử là 2^n
Thật vậy, bằng quy nạp ta có :
Với n=0, tập rỗng có 2^0=1 tập con. Đúng.
Với n=1, có 2^1 = 2 tập con là rỗng và chính nó. Đúng.
Giả sử công thức đúng với n=k. Tức là số tập con của tập hợp gồm k phần tử là 2^k
Ta phải chứng minh công thức đúng với k+1.
Ngoài 2^k tập con vốn có, thêm cho mỗi tập cũ phần tử thứ k + 1 thì được một tập con mới. Vậy ta được 2^k tập con mới. Tổng số tập con của tập hợp gồm k + 1 phần tử (tức tổng số tập con của tập gồm 2^k phần tử và tập con mới tạo thành) là : 2^k + 2^k = 2^k . 2 = 2 ^(k+1). Đúng
Vậy số tập con của tập A gồm n phần tử là 2^n
đúng ko bn
nếu **** thì tk mk nha
:3

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
Do đó: AEHF là hình chữ nhật

\(1,\\ a,\Rightarrow x^2-x-x^2+2x+3=7\\ \Rightarrow x=4\\ b,\Rightarrow\left(x+1\right)^2=9\Rightarrow\left[{}\begin{matrix}x+1=3\\x+1=-3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-4\end{matrix}\right.\\ c,\Rightarrow x^2\left(x-5\right)+4\left(x-5\right)=0\\ \Rightarrow\left(x^2+4\right)\left(x-5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=-4\left(vô.lí\right)\\x=5\end{matrix}\right.\Rightarrow x=5\\ 2,\\ a^3+b^3=\left(a+b\right)^3-3ab\left(a+b\right)\\ =\left(-1\right)^3-3\left(-1\right)\left(-6\right)=-1-18=-19\)

Bài 2:
a: \(x^2-4x+3=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
b: \(\left(3x-5\right)^2-\left(x+1\right)^2=0\)
\(\Leftrightarrow\left(3x-5-x-1\right)\left(3x-5+x+1\right)=0\)
\(\Leftrightarrow\left(4x-4\right)\left(2x-6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)
Bài 1:
a: \(2x^3-8x=2x\left(x^2-4\right)=2x\left(x-2\right)\left(x+2\right)\)
b: \(x\left(x-y\right)+x^2-y^2\)
\(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)
\(=\left(x-y\right)\left(2x+y\right)\)
b: \(25\left(x+5\right)^2-9\left(x+7\right)^2\)
\(=\left(5x+25\right)^2-\left(3x+21\right)^2\)
\(=\left(5x+25-3x-21\right)\left(5x+25+3x+21\right)\)
\(=\left(2x+4\right)\left(8x+46\right)\)
\(=4\left(x+2\right)\left(4x+23\right)\)

Bài 1:
a: \(M=2\left(x^2-\dfrac{7}{2}x+\dfrac{9}{2}\right)\)
\(=2\left(x^2-2\cdot x\cdot\dfrac{7}{4}+\dfrac{49}{16}+\dfrac{23}{16}\right)\)
\(=2\left(x-\dfrac{7}{4}\right)^2+\dfrac{23}{8}>0\)
b: \(=3\left(x^2-\dfrac{4}{3}x+\dfrac{11}{3}\right)\)
\(=3\left(x^2-2\cdot x\cdot\dfrac{2}{3}+\dfrac{4}{9}+\dfrac{29}{9}\right)\)
\(=3\left(x-\dfrac{2}{3}\right)^2+\dfrac{29}{3}>0\)

2. a. x3 - 9x2 + 27x - 27 tại x = 5
= x3 - 3.x2.3 + 3.x.32 - 33
= (x - 3)3
Thay x = 5 vào phép tính:
= (5 - 3)3
= 23
= 8

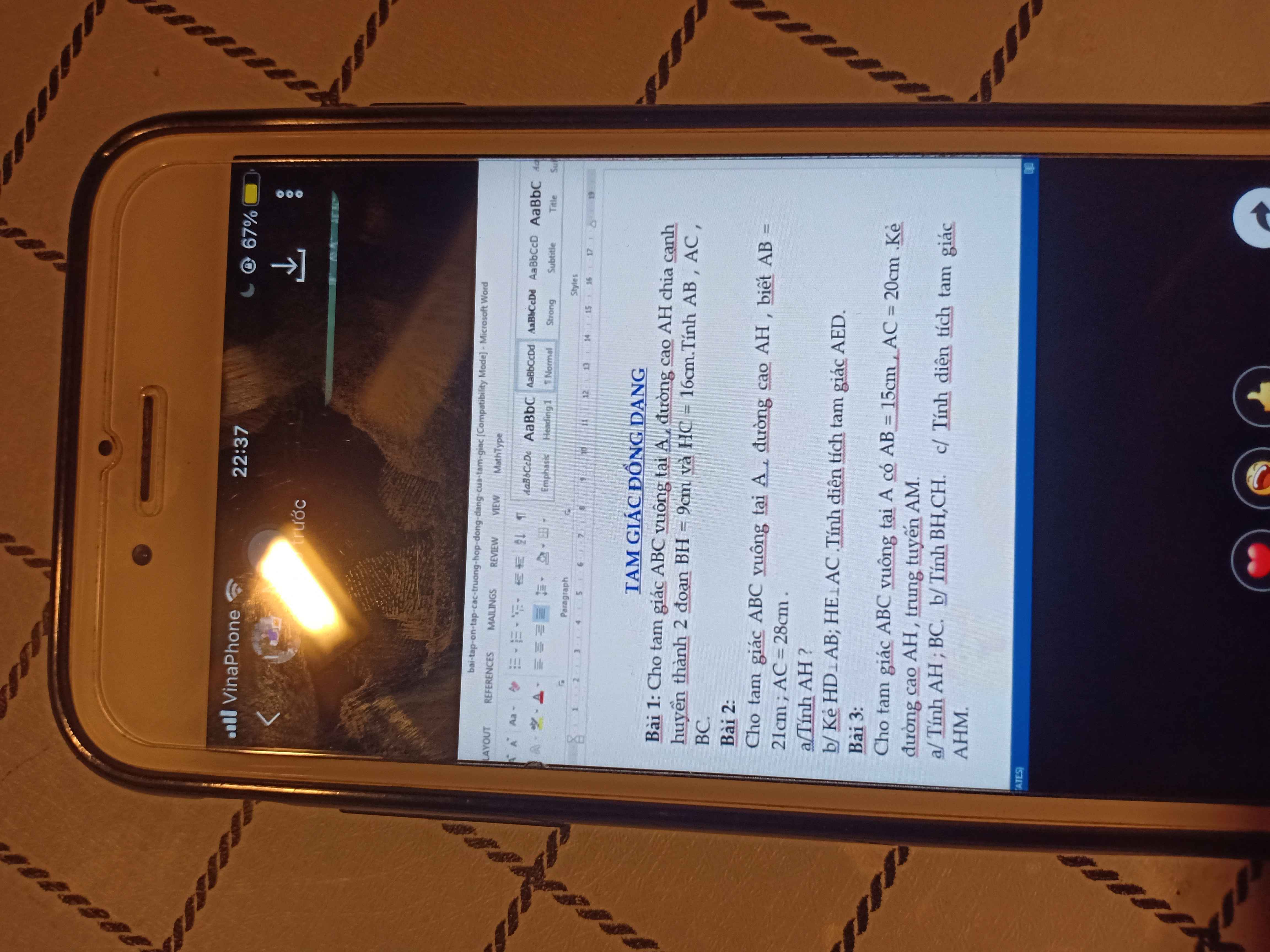
Bài 1:
Ta có: BC=BH+HC
nên BC=9+16
hay BC=25cm
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB^2=9\cdot25\\AC^2=16\cdot25\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=15cm\\AC=20cm\end{matrix}\right.\)

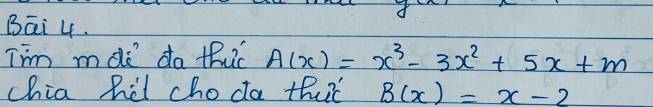 sossssssssssss gấp
sossssssssssss gấp
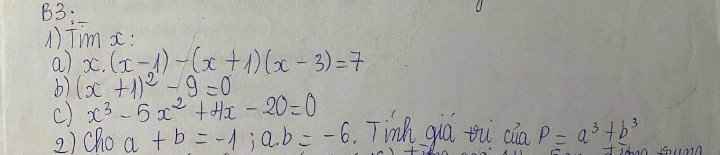




Do A(x) chia hết cho \(B\left(x\right)=x-2\)
Nên A(x) sẽ nhận \(x=2\) là nghiệm thay vào ta có:
\(2^3-3\cdot2^2+5\cdot2+m=0\)
\(\Leftrightarrow8-3\cdot4+10+m=0\)
\(\Leftrightarrow18-12+m=0\)
\(\Leftrightarrow6+m=0\)
\(\Leftrightarrow m=-6\)
Vậy khi m=-6 thì A(x) chia hết cho B(x)