K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
LV
3
12 tháng 2 2023
phương trình tích là phương trình có dạng A*B=0
=>A=0 hoặc B=0
NT
1
2 tháng 6 2019
Anh làm cách cosi
\(VT^2=\frac{a^2b^2}{c^2}+\frac{b^2c^2}{a^2}+\frac{a^2c^2}{b^2}+2\left(b^2+a^2+c^2\right)\)
Ta có \(\frac{a^2b^2}{c^2}+\frac{b^2c^2}{a^2}\ge2b^2\)
\(\frac{b^2c^2}{a^2}+\frac{a^2c^2}{b^2}\ge2c^2\)=> \(\frac{a^2b^2}{c^2}+\frac{b^2c^2}{a^2}+\frac{a^2c^2}{b^2}\ge a^2+b^2+c^2\)
\(\frac{a^2c^2}{b^2}+\frac{a^2b^2}{c^2}\ge2c^2\)
=> \(VT^2\ge3\left(a^2+b^2+c^2\right)=9\)
=> \(VT\ge3\)
Dấu bằng xảy ra khi a=b=c1
CB
2 tháng 6 2019
xD
Có: \(\frac{ab}{c}+\frac{bc}{a}+\frac{ac}{b}\ge3\)(1)
\(\Leftrightarrow\frac{a^2b^2}{c^2}+\frac{b^2c^2}{a^2}+\frac{a^2c^2}{b^2}+2\left(a^2+b^2+c^2\right)\ge9\)
\(\Leftrightarrow\frac{\left(ab\right)^3+\left(bc\right)^3+\left(ac\right)^3-3a^2b^2c^2}{a^2b^2c^2}\ge0\)
Đặt \(\hept{\begin{cases}ab=x\\bc=y\\ac=z\end{cases}\left(x,y,z>0\right)}\)
\(\left(1\right)\Leftrightarrow\frac{x^3+y^3+z^3-3xyz}{\left(abc\right)^2}\ge0\)
\(\Leftrightarrow\frac{\frac{1}{2}\left(x+y+z\right)\left[\left(x-y\right)^2+\left(y-z\right)^2+\left(x-z\right)^2\right]}{\left(abc\right)^2}\ge0\)(đúng)
Vậy ........... dấu = xảy ra khi và chỉ khi x=y=z hay a=b=c=1
15 tháng 10 2023
a: Xét tứ giác AMND có
AM//ND
AM=ND
Do đó: AMND là hình bình hành
Hình bình hành AMND có AM=AD(\(=\dfrac{AB}{2}\))
nên AMND là hình thoi
Xét tứ giác BMNC có
BM//NC
BM=NC
Do đó: BMNC là hình bình hành
Xét hình bình hành BMNC có \(MB=BC\left(=\dfrac{AB}{2}\right)\)
nên BMNC là hình thoi
b:
AMND là hình thoi
=>\(MN=AD=\dfrac{DC}{2}\)
Xét ΔDMC có
MN là đường trung tuyến
\(MN=\dfrac{DC}{2}\)
Do đó: ΔDMC vuông tại M
=>\(\widehat{DMC}=90^0\)
c: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
=>AN//CM
NT
4
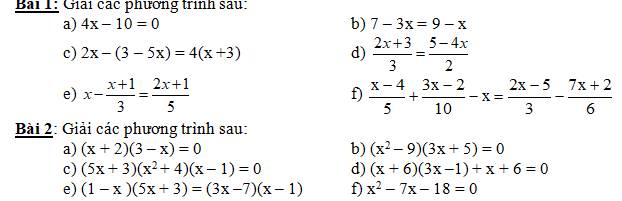
1) a) 4x-10=0
4x=10
=>x=2,5
b) 7-3x=9-x
7-3x=-(3x-7)
-2x=2
=>x=-1
c) 2x-(3-5x)=4(x+3)
7x-3=4(x+3)
7x-3=4x+12
=>3x=15
=>x=5
d) 2x+3/3=5-4x/2
=>(2x+3)2=3(5-4x)
=>x=19/6
Những câu nào mình chưa trl thì bạn chia từng câu r đăng nhé