K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
MH
25 tháng 1 2022
Ta có:
\(7^{39}< 7^{40}=49^{20}\)
\(51^{20}>49^{20}\)
⇒ \(7^{39}< 51^{20}\)
MP
1
7 tháng 1 2019
tự làm đi mình 0 có biết với lại mình đang bận đừng hỏi mình bạn có giúp mình thì giúp mình cảm ơn
PT
1
CM
19 tháng 5 2019
a) 1024 9 = ( 2 10 ) 9 = 2 90 < 2 100
b) 6 . 5 29 > 5 . 5 29 = 5 30
c) 10 30 = ( 10 3 ) 10 = 1000 10 ; 2 100 = ( 2 10 ) 10 = 1024 10 n ê n 10 30 < 2 100 .
AU
0
PT
1
CM
14 tháng 7 2017
a) Cách 1: 2 100 = 2 10 10 = 1024 10 > 1024 9
Cách 2: 1024 9 = 2 10 9 = 2 90 < 2 100
b) 6 . 5 29 > 5 . 5 29 = 5 30
c) 2 98 = 2 2 49 = 4 49 < 9 49
d) 10 30 = 10 3 10 = 1000 10 ; 2 100 = 2 10 10 = 1024 10 nên 10 30 < 2 100
17 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
`2^100` và `3^50`
Ta có:
\(2^{100}=\left(2^4\right)^{25}=16^{25}\)
\(3^{50}=\left(3^2\right)^{25}=9^{25}\)
Vì `16 > 9 =>`\(16^{25}>9^{25}\Rightarrow2^{100}>3^{50}\)
Vậy, `2^100 > 3^50` `.`
H9
HT.Phong (9A5)
CTVHS
18 tháng 7 2023
Sao không so sánh \(4^{50}\) với \(3^{50}\) cho nhanh nhỉ
2 tháng 8 2023
Ta có: 2100=231.269
= 231 . 263 . 26
= 231 . ( 29 )7 . ( 22)3
= 231 . 5127 . 43
Lại có : 1031 = 231 . 531
= 231 . 528 . 53
= 231 . ( 54) 7 . 53
= 231 . 6257 . 53
=>231 . 6257 . 53 > 231 . 3127 . 53 > 231 . 3127 . 43
<=> 2100<1031
VN
Võ Ngọc Phương
VIP
15 tháng 10 2023
Ta có:
\(2^{200}.2^{100}=\left(2^2\right)^{100}.2^{100}=4^{100}.2^{100}=\left(4.2\right)^{100}=8^{100}\)
\(3^{100}.3^{100}=\left(3.3\right)^{100}=9^{100}\)
Vì \(8< 9\) nên \(8^{100}< 9^{100}\)
Vậy \(2^{200}.2^{100}< 3^{100}.3^{100}\)
\(#WendyDang\)
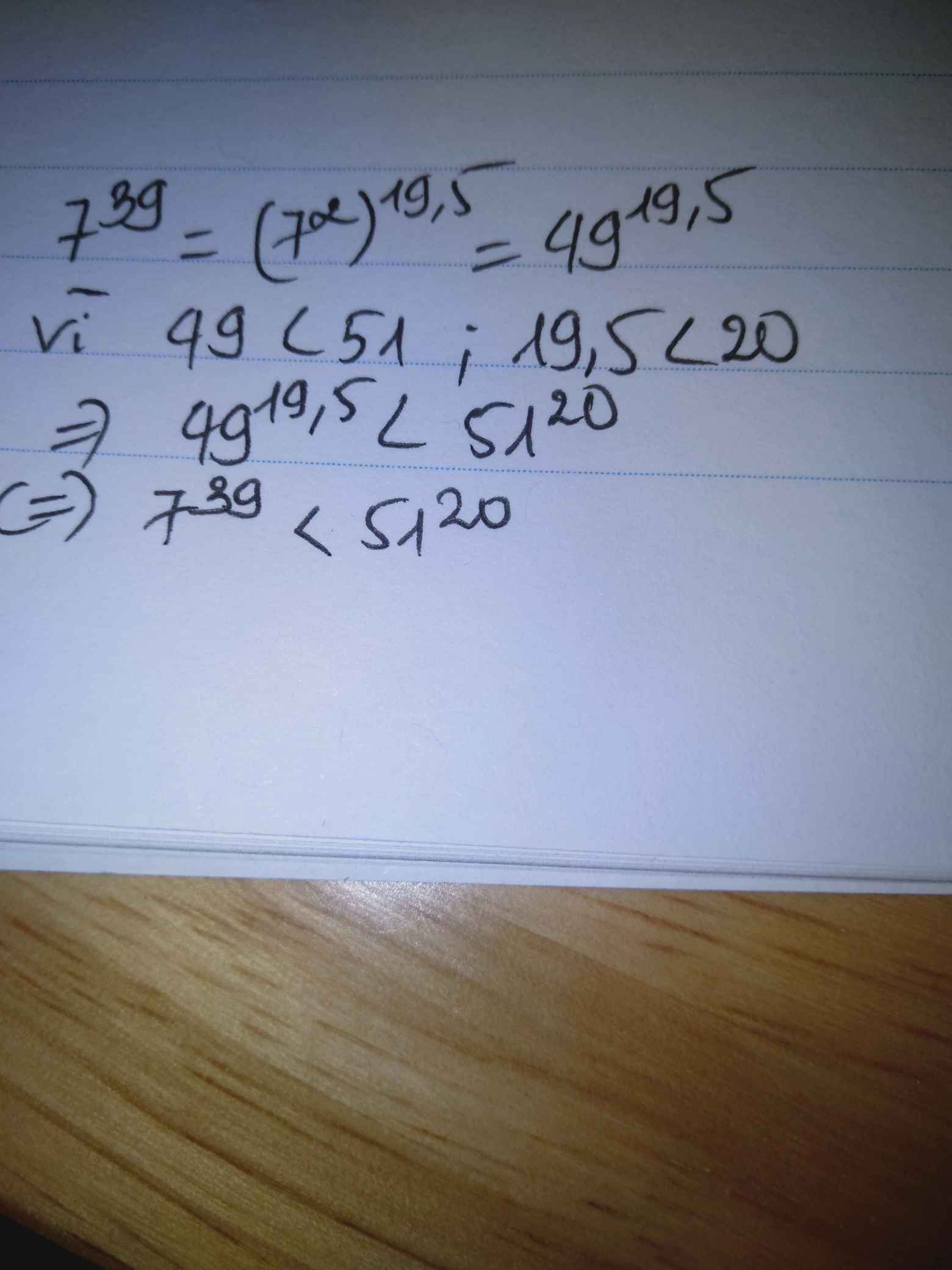
\(7.2^{100}< 8.2^{100}=2^3.2^{100}=2^{103}\)
cảm ơn nhìu ạ