K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
9 tháng 9 2021
\(27^{13}=\left(3^3\right)^{13}=3^{39};243^8=\left(3^5\right)^8=3^{40};3^{39}< 3^{40}\Rightarrow27^{13}< 243^8\\ 125^{80}=\left(5^3\right)^{80}=5^{240};25^{118}=\left(5^2\right)^{118}=5^{236};5^{240}>5^{236}\Rightarrow125^{80}>25^{118}\)
10 tháng 3 2021
a) Ta có \(\overline{2021ab}⋮31\Leftrightarrow202100+\overline{ab}⋮31\Leftrightarrow11+\overline{ab}⋮31\Leftrightarrow\overline{ab}\in\left\{20;51;82\right\}\).
Vậy..
VN
3
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
11 tháng 3 2021
a/
\(\overline{2021ab}=202100+\overline{ab}=6519.31+11+\overline{ab}⋮31\)
\(6519.31⋮31\Rightarrow11+\overline{ab}⋮31\)
=> \(\overline{ab}=20\) hoặc \(\overline{ab}=51\) hoặc \(\overline{ab}=82\)
b/ 536 chia b dư 11; 2713 chia b dư 13 nên b>13
\(536-11=525⋮b\Rightarrow5.525=2625⋮b\)
\(2713-13=2700⋮b\)
\(\Rightarrow2700-2625=75⋮b\)
=> b=5 hoặc b=25 hoặc b=75. Do b>13 => b=25 hoặc b=75
25 tháng 2 2023
a: 43/52>26/52=1/2=60/120
b: 17/68=1/4<1/3=35/105<35/103
c: \(\dfrac{2018\cdot2019-1}{2018\cdot2019}=1-\dfrac{1}{2018\cdot2019}\)
\(\dfrac{2019\cdot2020-1}{2019\cdot2020}=1-\dfrac{1}{2019\cdot2020}\)
2018*2019<2019*2020
=>-1/2018*2019<-1/2019*2020
=>\(\dfrac{2018\cdot2019-1}{2018\cdot2019}< \dfrac{2019\cdot2020-1}{2019\cdot2020}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
10 tháng 5 2023
\(\dfrac{19}{19}\) = 1 < \(\dfrac{2005}{2004}\) vậy \(\dfrac{19}{19}\) < \(\dfrac{2005}{2004}\)
\(\dfrac{72}{73}\) = 1 - \(\dfrac{1}{73}\)
\(\dfrac{98}{99}\) = 1 - \(\dfrac{1}{99}\)
Vì \(\dfrac{1}{73}\) > \(\dfrac{1}{99}\) nên \(\dfrac{72}{73}\) < \(\dfrac{98}{99}\)
21 tháng 2 2022
a) ta có: \(1-\frac{2012}{2013}=\frac{1}{2013}\)
\(1-\frac{2013}{2014}=\frac{1}{2014}\)
mà \(\frac{1}{2013}>\frac{1}{2014}\) nên \(\frac{2013}{2014}>\frac{2012}{2013}\)
PT
1
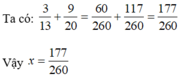
9^20 > 27^13 ( t...i...c...k n...h...a )
920>2713
Có cần cách làm ko?