K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CM
3 tháng 9 2019
Sơ đồ con đường |
Lời giải chi tiết |
|
Ta có: ( 6 100 − 1 ) = ( 6 − 1 ) ( 6 99 + ... + 1 ) = 5 ( 6 99 + ... + 1 ) ⋮ 5 |
4 tháng 3 2021
Đặt \(A=6^2+6^4+6^6+...+6^{98}+6^{100}\)
Ta có: \(A=6^2+6^4+6^6+...+6^{98}+6^{100}\)
\(\Leftrightarrow36A=6^4+6^6+...6^{100}+6^{102}\)
\(\Leftrightarrow A-36A=6^2+6^4+6^6+...6^{98}+6^{100}-6^4-6^6-...-6^{100}-6^{102}\)
\(\Leftrightarrow-35\cdot A=6^2-6^{102}\)
\(\Leftrightarrow A=\dfrac{6^{102}-6^2}{35}\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
22 tháng 8 2023
C = 1 + 6 + 62+ 63+...+ 6100
6C = 6 + 62+ 63 +...+ 6100 + 6101
6C - C = 6101 - 1
5C = 6101 - 1
C = \(\dfrac{6^{101}-1}{5}\)
22 tháng 8 2023
\(C=1+6+6^2+...+6^{100}\)
\(\Rightarrow C=\dfrac{6^{100+1}-1}{6-1}\)
\(\Rightarrow C=\dfrac{6^{101}-1}{5}\)
NL
2
6 tháng 1
Ta có:
\(\dfrac{37}{-49}< 0;\dfrac{-12}{-35}=\dfrac{12}{35}>0\)
\(\Rightarrow\dfrac{37}{-49}< \dfrac{-12}{-35}\)
Vậy...
LK
1
mik mới so sánh được với 98 thôi. Mik ra kq là A > 99 - 99/100 -> A > 98 chứ chưa so sánh đc với 99.
5 tháng 6 2021
`A=3/4+8/9+.............+9999/10000`
`=1-1/4+1-1/9+,,,,,,,,,,+1-1/10000`
`=99-(1/4+1/9+.........+1/10000)<99-0=99`
`=>A<99`
HQ
Hà Quang Minh
Giáo viên
7 tháng 10 2023
a) Ta có: \( - 2 = \frac{{ - 2}}{1} = \frac{{ - 40}}{{20}}\)
\(\frac{{ - 11}}{5} = \frac{{ - 44}}{{20}} < \frac{{ - 40}}{{20}}\) nên \(\frac{{ - 11}}{5} < -2\).
\(\frac{{ - 7}}{4} = \frac{{ - 7.5}}{{4.5}} = \frac{{ - 35}}{{20}} > \frac{{ - 40}}{{20}}\) nên \(\frac{{ - 7}}{4} > -2\)
Vậy \(\frac{{ - 11}}{5} < \frac{{ - 7}}{4}\).
b) Ta có: \(\frac{{2020}}{{ - 2021}} = \frac{{ - 2020}}{{2021}} > \frac{{ - 2022}}{{2021}}\)
Vậy \(\frac{{2020}}{{ - 2021}} > \frac{{ - 2022}}{{2021}}\)
T
2
31 tháng 7 2023
\(A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}\)
\(\dfrac{1}{2.2}< \dfrac{1}{1.2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3.3}< \dfrac{1}{2.3}=\dfrac{1}{2}-\dfrac{1}{3}\)
\(\dfrac{1}{4.4}< \dfrac{1}{3.4}=\dfrac{1}{3}-\dfrac{1}{4}\)
...
\(\dfrac{1}{2009.2009}< \dfrac{1}{2008.2009}=\dfrac{1}{2008}-\dfrac{1}{2009}\)
\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)
\(\Rightarrow A=\dfrac{1}{2.2}+\dfrac{1}{3.3}+\dfrac{1}{4.4}+...+\dfrac{1}{2009.2009}< 1\)
31 tháng 7 2023
Ta có:
\(\dfrac{1}{2\times2}+\dfrac{1}{3\times3}+\dfrac{1}{4\times4}+...+\dfrac{1}{2009\times2009}< \dfrac{1}{1\times2}+\dfrac{1}{2\times3}+\dfrac{1}{3\times4}+...+\dfrac{1}{2008\times2009}\\ =1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{4}+...+\dfrac{1}{2008}-\dfrac{1}{2009}=1-\dfrac{1}{2009}< 1\)
LM
25 tháng 10 2021
a, 6100 - 1 = (6 . 6 . 6 ..... 6) - 1 = [(...6) . (...6) . (...6) ..... (...6)] - 1 = (...6) - 1 = ...5 \(⋮\) 5
LM
25 tháng 10 2021
b, 2120 - 1110 = (21 . 21 . 21 . 21 . 21..... 21) - (11 . 11 . 11 . 11 ..... 11) = [(...1) . (...1) . (...1) . (...1).....(...1)] - [(...1) . (...1) . (...1) . (...1).....(...1)] = (...1) - (...1) = ....0 \(⋮\) 2; \(⋮\) 5
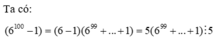
600100>3170
6^100 = 2^100 x 3^100 = 1024^10 x 3^100 3^170 = 3^100 x 3^70 = 3^100 x 2187^10 Vì 1024^10 < 2187^10 nên 1024^10 x 3^100 < 3^100 x 2187^10 hay 6^100 <33^170 Vậy 6^100 <3^170 tích cho mình nha