
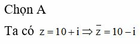
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

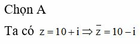

Đáp án D
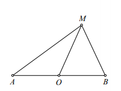 Hình vẽ minh họa
Hình vẽ minh họa
Gọi A(0;-1);B(0;1) có trung điểm là O(0;0). Điểm M biểu diễn số phức z
Theo công thức trung tuyến trong tam giác MAB thì z 2 = M O 2 = M A 2 + M B 2 2 - A B 2 4
Theo giả thiết, ta có 4MA + 2MB = 10.
Đặt M A = t ⇒ M B = 10 - 4 t 3
Vì M A - M B = 10 - 7 t 2 ≤ A B = 2 ⇒ - 6 ≤ 10 - 7 t ≤ 6 ⇔ a ∈ 4 7 ; 16 7
Ta có M A 2 + M B 2 = t 2 + 10 - 4 t 3 2 = 25 t 2 - 80 t + 100 9 = 5 t - 8 2 + 36 9
Do - 36 7 ≤ 5 t - 8 ≤ 34 7 ⇒ 0 ≤ 5 t - 8 2 ≤ 1296 49 ⇒ M A 2 + M B 2 ≥ 4 nên z 2 ≥ 1 ⇒ m = z m i n = 1 .

Đáp án D
4 | z + i | + 3 | z − i | = 10 = > 4 x 2 + ( y + 1 ) 2 + 3 x 2 + ( y − 1 ) 2 = 10 = > 4 M A + 3 M B = 10 ( M ( x , y ) ; A ( 0 , − 1 ) ; B ( 0 , 1 ) ) = > M O 2 = M A 2 + M B 2 2 − A B 2 4 < = > M O 2 = M A 2 + M B 2 2 − 1
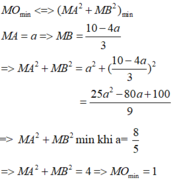

Phương pháp:
Tìm tập hợp các điểm biểu diễn số phức bài cho sau đó tính diện tích hình phẳng được giới hạn bởi các điểm đó.
Cách giải:
