Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Leftrightarrow n^5+n^2-n^2+1⋮n^3+1\)
\(\Leftrightarrow-n^3+n⋮n^3+1\)
\(\Leftrightarrow n=1\)

\(\sqrt{12-6\sqrt{3}}=\sqrt{9-6\sqrt{3}+3}=\sqrt{3^2-2.3.\sqrt{3}+\left(\sqrt{3}\right)^2}=\sqrt{\left(3-\sqrt{3}\right)^2}\)
\(=\left|3-\sqrt{3}\right|=3-\sqrt{3}\)
\(\sqrt{19+8\sqrt{3}}=\sqrt{16+8\sqrt{3}+3}=\sqrt{4^2+2.4.\sqrt{3}+\left(\sqrt{3}\right)^2}=\sqrt{\left(4+\sqrt{3}\right)^2}\)
\(=\left|4+\sqrt{3}\right|=4+\sqrt{3}\)
\(\sqrt{14-6\sqrt{5}}=\sqrt{9-6\sqrt{5}+5}=\sqrt{3^2-2.3.\sqrt{5}+\left(\sqrt{5}\right)^2}=\sqrt{\left(3-\sqrt{5}\right)^2}\)
\(=\left|3-\sqrt{5}\right|=3-\sqrt{5}\)
\(\sqrt{12-6\sqrt{3}}=\sqrt{3^2-2.3.\sqrt{3}+\left(\sqrt{3}\right)^2}=\sqrt{\left(3-\sqrt{3}\right)^2}=\left|3-\sqrt{3}\right|=3-\sqrt{3}\)
\(\sqrt{19+8\sqrt{3}}=\sqrt{4^2+2.4.\sqrt{3}+\left(\sqrt{3}\right)^2}=\sqrt{\left(4+\sqrt{3}\right)^2}=\left|4+\sqrt{3}\right|=4+\sqrt{3}\)
\(\sqrt{14-6\sqrt{5}}=\sqrt{3^2-2.3.\sqrt{5}+\left(\sqrt{5}\right)^2}=\sqrt{\left(3-\sqrt{5}\right)^2}=\left|3-\sqrt{5}\right|=3-\sqrt{5}\)

Vào địa chỉ http://h.vn/vip/tuan_2468 bạn ấy đăng bài này đấy không được thì vào http://h.vn/?l=user.display.profile là sẽ có cho mình li ke nhé

\(\Leftrightarrow\left\{{}\begin{matrix}5x=10\\2x-y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2x-3=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2x-3\\3x+2x-3=7\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=2x-3\\5x=10\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=2.2-3\\x=2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)

a.
Khi \(x=4\Rightarrow A=\dfrac{1}{\sqrt{4}}+\dfrac{\sqrt{4}}{\sqrt{4}+1}=\dfrac{1}{2}+\dfrac{2}{3}=\dfrac{7}{6}\)
b.
\(B=\dfrac{1}{3}\Rightarrow\dfrac{\sqrt{x}}{x+\sqrt{x}}=\dfrac{1}{3}\)
\(\Rightarrow3\sqrt{x}=x+\sqrt{x}\)
\(\Rightarrow x-2\sqrt{x}=0\)
\(\Rightarrow\sqrt{x}\left(\sqrt{x}-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{x}=0\\\sqrt{x}=2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
c.
\(P=A:B=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{x+\sqrt{x}}\right)\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}\left(\sqrt{x}+1\right)}\right)\)
\(=\dfrac{\left(x+\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
\(P>3\Rightarrow\dfrac{x+\sqrt{x}+1}{\sqrt{x}}>3\)
\(\Leftrightarrow x+\sqrt{x}+1>3\sqrt{x}\) (do \(\sqrt{x}>0\))
\(\Leftrightarrow x-2\sqrt{x}+1>0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2>0\)
\(\Leftrightarrow\sqrt{x}-1\ne0\)
\(\Rightarrow x\ne1\)
Kết hợp ĐKXĐ ta được: \(\left\{{}\begin{matrix}x>0\\x\ne1\end{matrix}\right.\)
anh ơi https://hoc24.vn/cau-hoi/giai-phuong-trinh-nghiem-nguyen-saux2x-y20.1353640161947
-> giải thích hộ cái bảng của a tính thế nào vs ạ
có bao nhiêu số chính phương có ba chử số
A 23
B 24
C 25
D 26
các bạn giải chi tiết giùm mình luôn nha!!!

Gọi k là số số chính phương có 3 chữ số => 100 <= k <= 999
<=> 10 <= √k <= 31 ( √k thuộc N )
Vậy có 24 số chính phương có 3 chữ số bắt đầu từ 10^2 tới 31^2

2:
1+cot^2a=1/sin^2a
=>1/sin^2a=1681/81
=>sin^2a=81/1681
=>sin a=9/41
=>cosa=40/41
tan a=1:40/9=9/40
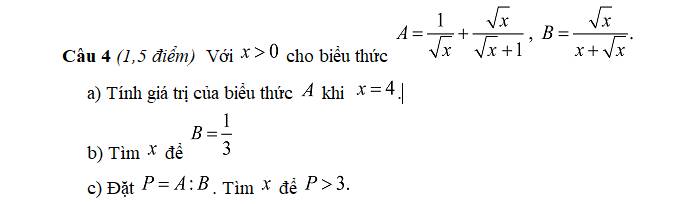

D nhé bn
cắc là câu d
ai ủng hộ thì k cho nhé