
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2sin^2\dfrac{x}{2}=cos5x+1\)
\(\Leftrightarrow-cos5x=1-2.sin^2\dfrac{x}{2}\)
\(\Leftrightarrow-cos5x=cosx\)
\(\Leftrightarrow cos\left(5x\right)=cos\left(\pi-x\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}5x=\pi-x+k2\pi\\5x=-\pi+x+k2\pi\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+\dfrac{k\pi}{3}\\x=-\dfrac{\pi}{4}+\dfrac{k\pi}{2}\end{matrix}\right.\) (k nguyên)
Vậy..

Có: y=sin^4x−cos^4x
= (sin^2x−cos^2x)(sin^2x+cos^2x)
= −cos2x
=> −1≤y≤1
=> min y=−1⇔cos2x=1⇔x=kπ
max y=1⇔cos2x=−1⇔x=π2+kπ
Vậy min y = -1; max y=1
\(y=\left(sin^2x+cos^2x\right)^2-2sin^2x.cos^2x+sin2x\)
\(=1-\dfrac{1}{2}sin^22x+sin2x\)
Đặt \(sin2x=t\in\left[-1;1\right]\Rightarrow y=f\left(t\right)=-\dfrac{1}{2}t^2+t+1\)
\(-\dfrac{b}{2a}=1\) ; \(f\left(-1\right)=-\dfrac{1}{2}\) ; \(f\left(1\right)=\dfrac{3}{2}\)
\(\Rightarrow y_{min}=-\dfrac{1}{2}\) khi \(sin2x=-1\)
\(y_{max}=\dfrac{3}{2}\) khi \(sin2x=1\)


\(\begin{array}{l}a)\;sin2x + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) + cos3x = 0\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = - cos3x\\ \Leftrightarrow cos\left( {\frac{\pi }{2} - 2x} \right) = cos\left( {\pi - 3x} \right)\\ \Leftrightarrow \left[ \begin{array}{l}\frac{\pi }{2} - 2x = \pi - 3x + k2\pi \\\frac{\pi }{2} - 2x = - \pi + 3x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{2} + k2\pi \\x = \frac{{3\pi }}{{10}} + k\frac{{2\pi }}{5}\end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}b)\;sinx.cosx = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow \frac{1}{2}\;sin2x = \frac{{\sqrt 2 }}{4}\\ \Leftrightarrow sin2x = \frac{{\sqrt 2 }}{2} = sin\left( {\frac{\pi }{4}} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x = \frac{\pi }{4} + k2\pi \\2x = \pi - \frac{\pi }{4} + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \frac{\pi }{8} + k\pi \\x = \frac{{3\pi }}{8} + k\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
\(\begin{array}{l}c)\;sinx + sin2x = 0\\ \Leftrightarrow sinx = - sin2x\\ \Leftrightarrow sinx = sin( - 2x)\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2x + k2\pi \\x = \pi + 2x + k2\pi \end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = k\frac{{2\pi }}{3}\\x = - \pi + k2\pi \end{array} \right.\left( {k \in \mathbb{Z}} \right)\end{array}\)
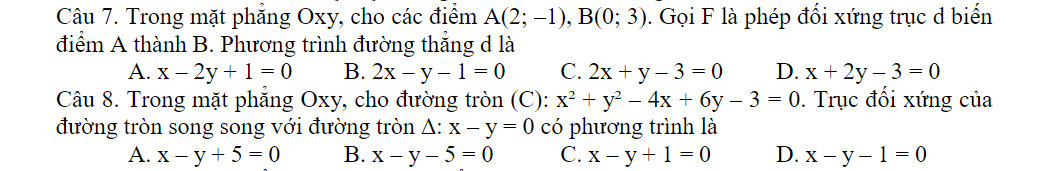 Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều
Làm giúp mình 2 bài này với, có giải chi tiết. Mình cảm ơn nhiều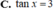
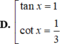

\(sin^2x+\sqrt{3}sinxcosx=1\)
\(\Leftrightarrow sin^2x+\sqrt{3}sinxcosx=sin^2x+cos^2x\)
\(\Leftrightarrow cosx\left(\sqrt{3}sinx-cosx\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}cosx=0\\\sqrt{3}sinx=cosx\end{cases}}\Leftrightarrow\orbr{\begin{cases}cosx=0\\tanx=\frac{1}{\sqrt{3}}\end{cases}}\)
Từ đây suy ra nghiệm.