Trong hình 67, cung AmB có số đo là 60o. Hãy:Vẽ góc ở tâm chắn cung AmB. Tính...

K

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

PT

Pham Trong Bach

3 tháng 7 2019

Trong hình 67, cung AmB có số đo là 60o. Hãy:

Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.

1

CM

Cao Minh Tâm

3 tháng 7 2019

Giải bài 89 trang 104 SGK Toán 9 Tập 2 | Giải toán lớp 9

Các câu hỏi dưới đây có thể giống với câu hỏi trên

PT

Pham Trong Bach

29 tháng 7 2019

Trong hình 67, cung AmB có số đo là 60 ° . Hãy:a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ADB và ACB e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh...

1

CM

Cao Minh Tâm

29 tháng 7 2019

Giải bài 89 trang 104 SGK Toán 9 Tập 2 | Giải toán lớp 9

Giải bài 89 trang 104 SGK Toán 9 Tập 2 | Giải toán lớp 9

Giải bài 89 trang 104 SGK Toán 9 Tập 2 | Giải toán lớp 9

PT

Pham Trong Bach

11 tháng 7 2018

Trong hình 67, cung AmB có số đo là 60o. Hãy:

Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.

1

CM

Cao Minh Tâm

11 tháng 7 2018

Giải bài 89 trang 104 SGK Toán 9 Tập 2 | Giải toán lớp 9

SG

Sách Giáo Khoa

13 tháng 4 2017

Hình viên phân là phần hình tròn giới hạn bởi một cung và dây căng cung ấy. Hãy tính diện tích hình viên phân AmB, biết góc ở tâm \(\widehat{AOB}=60^o\) và bán kính đường tròn là 5,1 cm.

1

TT

Thien Tu Borum

13 tháng 4 2017

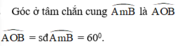
Hướng dẫn giải:

∆OAB là tam giác đều có cạnh bằng R = 5,1cm. Áp dụng công thức tính diện tích tam giác đều cạnh a là a2√44 ta có

S_∆OBC= SΔOBC=R2√34 (1)

Diện tích hình quạt tròn AOB là:

π.R2.6003600=πR26 (2)

Từ (1) và (2) suy ra diện tích hình viên phân là:

πR26−R2√34=R2(π6−√34)

Thay R = 5,1 ta có S_{viên phân}≈ 2,4 (cm²)

SG

Sách Giáo Khoa

11 tháng 4 2017

Hai tiếp tuyến của đường tròn (O) tại A và B cắt nhau tại M. Biết \(\widehat{AMB}=35^o.\)

a) Tính số đo của góc ở tâm tạo bở hai bán kính OA, OB.

b) Tính số đo mỗi cung AB (cung lớn và cung nhỏ).

1

OZ

¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O.o°¨

11 tháng 4 2017

a) Trong tứ giác AOBM có = = .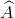

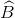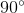Suy ra cung AMB + =

=> cung AMB= -

= -

=

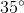
b) Từ 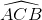= . Suy ra số đo cung nhỏ AB = và số đo cung lớn AB :

Cung AB = - =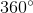

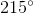
PT

Pham Trong Bach

21 tháng 10 2017

Trong hình 67, cung AmB có số đo là 60o. Hãy:

Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.

1

CM

Cao Minh Tâm

21 tháng 10 2017

Giải bài 89 trang 104 SGK Toán 9 Tập 2 | Giải toán lớp 9

SG

Sách Giáo Khoa

13 tháng 4 2017

Trong hình 67, cung AmB có số đo là 60o. Hãy: a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB. b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB. c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt. d) Vẽ góc ADB có đỉnh D ở trong đường tròn. So sánh \(\widehat{ADB}\) và \(\widehat{ACB}.\) e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So...

1

TT

Thien Tu Borum

13 tháng 4 2017

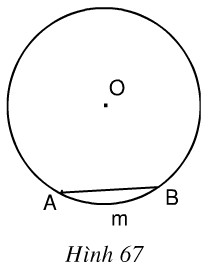
Trong hình 67, cung AmB có số đo là 66^o. Hãy:

a) Vẽ góc ở tâm chắn cung AmB. Tính góc AOB.

b) Vẽ góc nội tiếp đỉnh C chắn cung AmB. Tính góc ACB.

c) Vẽ góc tạo bởi tia tiếp tuyến Bt và dây cung BA. Tính góc ABt.

d) Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh ˆADBADB^ với ˆACBACB^ .

e) Vẽ góc AEB có đỉnh E ở bên ngoài đường tròn (E và C cùng phía đối với AB). So sánh ˆAEBAEB^ với ˆACBACB^

Hướng dẫn trả lời:

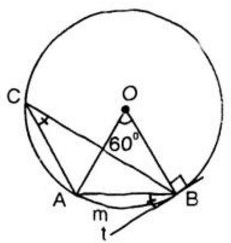
a) Từ O nối với hai đầu mút của cung AB

Ta có ˆAOBAOB^ là góc ở tâm chắn cung AB

Vì ˆAOBAOB^ là góc ở tân chắn cung AB nên

ˆAOBAOB^ = sđ cung AB = 60°

b) Lấy một điểm C bất kì trên (O). Nối C với hai đầu mút của cung AmB. Ta được góc nội tiếp ˆACBACB^

Khi đó: ˆACB=12sđcungAmB=12600=30ACB^=12sđcungAmB=12600=30

c) Vẽ bán kính OB. Qua B vẽ Bt ⊥ OB. Ta được góc Abt là góc tạo bởi tia tiếp tuyến Bt với dây cung BA.

Ta có: ˆABt=12sđcungAmB=300ABt^=12sđcungAmB=300

d) Lấy điểm D bất kì ở bên trong đường tròn (O). Nối D với A và D với B. ta được góc là góc ở bên trong đường tròn (O)

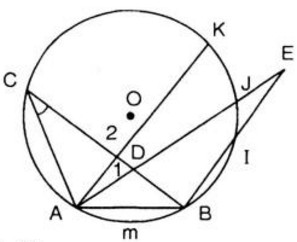
Ta có:

ˆACB=12sđcungAmBˆADB=12(sđcungAmB+sđcungCK)ACB^=12sđcungAmBADB^=12(sđcungAmB+sđcungCK)

Mà sđcung AmB + sđcung CK > sđcung AmB (do sđcung CK > 0) nên ˆADB>ˆACBADB^>ACB^

e) Lấy điểm E bất kì ở bên ngoài đường tròn, nối E với A và E với B, chúng cắt đường tròn lần lượt tại J và I.

Ta có góc AEB là góc ở bên ngoài đường tròn (O)

Có:

ˆACB=12sđcungAmBˆAEB=12(sđcungAmB−sđcungIJ)ACB^=12sđcungAmBAEB^=12(sđcungAmB−sđcungIJ)

Mà sđcung AmB – sđ cung IJ < sđcung AmB (do sđcung IJ > 0)

Nên ˆAEB<ˆACBAEB^<ACB^

TN

Trung Nguyễn Thành

27 tháng 12 2018 - olm

cho đường tròn tâm (O), đường kính AB, vẽ góc ở tâm \(\widehat{AOB}=50^o\) .Vẽ dây CD vuông góc vs AB và dây DE song song vs AB.

a) tính cung nhỏ \(\widebat{BC}\)

b) tính số đo cung \(\widebat{CBE}\) từ đó suy ra 3 điểm C, O ,E thẳng hàng

0

PT

Pham Trong Bach

30 tháng 11 2019

Trong hình 67, cung AmB có số đo là 60o. Hãy:

Vẽ góc ADB có đỉnh D ở bên trong đường tròn. So sánh A D B ^ v à A C B ^

1

CM

Cao Minh Tâm

30 tháng 11 2019

⇒ A B t ^ = 1 2 . s đ A B ⏜ + s đ M N ⏜ > 1 2 . s đ A B ⏜ = A C B ^

QH

Quang Hùng and Rum

25 tháng 3 2018 - olm

1. Cho tam giác ABC có A= 60o nội tiếp trong đường tròn (O;R)a) tính số đo cung BCb) tính độ dài dây cung BC và độ dài cung BC theo Rc) tính diện tích hình quạt ứng với góc ở tâm BOC theo R2. CHo (O;R) và dây AB= R\(\sqrt{2}\)a) tính số đo cung AB, số đo góc AOBb)| tính theo R độ dài cung ABtính diện tích của hình viên phân giới hạn bởi dây AB và cung nhỏ AB theo...

0