Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a, Tính được sđ B E ⏜ = 50 0
b, Chứng minh được sđ
C
B
E
⏜
=
180
0
=> C, O, E thẳng hàng (ĐPCM)

Tự vẽ hình
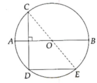
a) Do \(CD\) vuông góc \(AB\) nên \(AB\) là trung trực của \(CD\) (liên hệ giữa đường kính và dây cung)
\(\Rightarrow AC=AD\Rightarrow sđ\stackrel\frown{AC}=sđ\stackrel\frown{AD}\)
Mà \(sđ\stackrel\frown{AC}=\stackrel\frown{AOC}=50^0\Rightarrow sđ\stackrel\frown{AD}=50^0\).
Do \(DE\) song song \(AB\)
\(sđ\stackrel\frown{BE}=sđ\stackrel\frown{AD}=50^0\Rightarrow\widehat{BOE}=sđ\stackrel\frown{BE}=50^0\).
b) Do \(B\in\stackrel\frown{CE}\Rightarrow sđ\stackrel\frown{CBE}=sđ\stackrel\frown{CB}+sđ\stackrel\frown{BE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=\widehat{COB}+\widehat{BOE}=180^0-\widehat{AOC}+\widehat{BOE}\)
\(\Rightarrow sđ\stackrel\frown{CBE}=180^0-50^0+50^0=180^0\)
\(\Rightarrow\) CE là đường kính
\(\Rightarrow\) C, O, E thẳng hàng.

a) Ta có: AB//DE(gt)
CD⊥AB(gt)
Do đó: DE⊥CD(Định lí 2 từ vuông góc tới song song)
⇔\(\widehat{CDE}=90^0\)
Xét ΔCDE có \(\widehat{CDE}=90^0\)(cmt)
nên ΔCDE vuông tại D(Định nghĩa tam giác vuông)
⇔D nằm trên đường tròn đường kính CE
⇔C,D,E nằm trên đường tròn đường kính CE
mà C,D,E cùng nằm trên (O)(gt)
nên CE là đường kính của (O)
hay C,O,E thẳng hàng(đpcm)

a) Ta có \(\widehat{AND}=\widehat{AMD}\)(góc nội tiếp cùng chắn cung AD)
\(AM//BN\Rightarrow\widehat{AMN}=\widehat{MNB}\left(slt\right)\)
Ta có góc ANB nội tiếp đường trong O chắn nửa đường trong => góc ANB=900
Ta có: \(\widehat{AMD}+\widehat{AMN}+\widehat{DNM}=\widehat{DNM}+\widehat{AND}+\widehat{MNB}\)
\(\Leftrightarrow\widehat{DMN}+\widehat{MND}=90^0\Leftrightarrow\widehat{NDM}=90^0\)
Vì DM//AB và ND vuông góc với DM => DN vuông góc với AB
b) Ta có \(\widehat{BAN}=\widehat{BMN}\)(cùng chắn cung BN)
Mà \(\widehat{AMN}+\widehat{NMB}=90^0\Rightarrow\widehat{BAN}+\widehat{BAM}=90^0\Rightarrow\widehat{MAN}=90^0\)
\(\Rightarrow MANB\)là hcn
=> AM=BN
Ta có MC//AE và AM//EC => AMCE là hbh => AM=EC mà AM=BN => BN=EC mà BN//EC => ENBC là hbh =>EN//CB => CB vuông góc với AB(vì AB vuông góc với EN)=> BC là tiếp tuyến của đường tròn O
Chúc bạn học tốt!!!

